
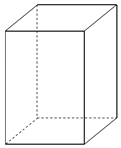
【題目】某工廠打算設計一種容積為2m3的密閉容器用于貯藏原料,容器的形狀是如圖所示的直四棱柱,其底面是邊長為x米的正方形,假設該容器的底面及側壁的厚度均可忽略不計.
(1)請你確定x的值,使得該容器的外表面積最小;
(2)若該容器全部由某種每平方米價格為100元的材料做成,且制作該容器僅需將購置的材料做成符合需要的矩形,這些矩形即是直四棱柱形容器的上下底面和側面(假設這一過程中產生的費用和材料損耗可忽略不計),再將這些上下底面和側面的邊緣進行焊接即可做成該容器,焊接費用是每米500元,試確定x的值,使得生產每個該種容器的成本(即原料購置成本+焊接費用)最低.
【答案】(1)當![]() 時,該容器的表面積最小.(2)當
時,該容器的表面積最小.(2)當![]() 時,生產每個容器的成本最低.
時,生產每個容器的成本最低.
【解析】
(1)設該容器高為h, 設該容器的外表面積為S,求出![]() ,再利用導數求函數的最小值得解;(2)設生產每個容器的成本為C(單位:元), 則
,再利用導數求函數的最小值得解;(2)設生產每個容器的成本為C(單位:元), 則![]() ,再利用導數求函數的最小值得解.
,再利用導數求函數的最小值得解.
(1)設該容器高為h,據體積為2m3得x2h=2,即![]() ,
,
設該容器的外表面積為S,則![]() ,
,
則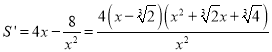 ,
,
令S′>0,解得![]() ,此時函數S(x)單調遞增,令S′<0,解得
,此時函數S(x)單調遞增,令S′<0,解得![]() ,此時函數S(x)單調遞減,
,此時函數S(x)單調遞減,
∴當![]() 時,該容器的表面積最小;
時,該容器的表面積最小;
(2)設生產每個容器的成本為C(單位:元),
則![]() ,
,
∴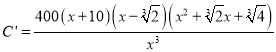 ,
,
令C′>0,解得![]() ,此時函數C(x)單調遞增,令C′<0,解得
,此時函數C(x)單調遞增,令C′<0,解得![]() ,此時函數C(x)單調遞減,
,此時函數C(x)單調遞減,
∴當![]() 時,生產每個容器的成本最低;
時,生產每個容器的成本最低;


 舉一反三同步巧講精練系列答案
舉一反三同步巧講精練系列答案科目:高中數學 來源: 題型:
【題目】近日,據《三秦都市報》消息稱陜西新高考方案初稿已經形成,新高考從2019年秋季入學的新高一學生開始執行“3+3”模式,即除語文、數學、外語三科為必考科目外,還要在物理、化學、生物、歷史、地理、政治六科中選擇三科作為選考科目.已知某生的高考志愿定為北京大學環境科學專業,按照2018年北大高考招生選考科目要求物理、化學必選,為該生安排課表(上午四節、下午四節,每門課每天至少一節課),現該生某天最后兩節為自習課,且數學不排下午第一節,語文、外語不相鄰(上午第四節和下午第一節不算相鄰),則該生該天課表不同的排法有________種.
查看答案和解析>>
科目:高中數學 來源: 題型:
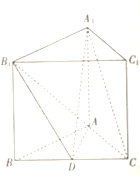
【題目】如圖,在三棱柱![]() 中,
中,![]() 平面
平面![]() ,
,![]() 為
為![]() 邊上一點,
邊上一點,![]() ,
,![]() .
.
(1)證明:平面![]() 平面
平面![]() .
.
(2)若![]() ,試問:
,試問:![]() 是否與平面
是否與平面![]() 平行?若平行,求三棱錐
平行?若平行,求三棱錐![]() 的體積;若不平行,請說明理由.
的體積;若不平行,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的導函數為
的導函數為![]() ,且對任意的實數x都有
,且對任意的實數x都有![]() (e是自然對數的底數),且
(e是自然對數的底數),且![]() ,若關于x的不等式
,若關于x的不等式![]() 的解集中恰有兩個整數,則實數m的取值范圍是( )
的解集中恰有兩個整數,則實數m的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,以
中,以![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立的極坐標系中,直線
軸的正半軸為極軸建立的極坐標系中,直線![]() 的極坐標方程為
的極坐標方程為![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為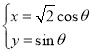 (
(![]() 為參數).
為參數).
(1)寫出直線![]() 及曲線
及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)過點![]() 且平行于直線
且平行于直線![]() 的直線與曲線
的直線與曲線![]() 交于
交于![]() ,
,![]() 兩點,若
兩點,若![]() ,求點
,求點![]() 的軌跡及其直角坐標方程.
的軌跡及其直角坐標方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知點A1,A2,…,An,…B1,B2,…,Bn,…均在拋物線x=y2上,線段AnBn與x軸的交點為Hn.將△OA1B1,△H1A2B2,…,△HnAn+1Bn+1,…的面積分別記為S1,S2,…,Sn+1,….已知上述三角形均為等腰直角三角形,且它們的頂角分別為O,H1,…,Hn,….
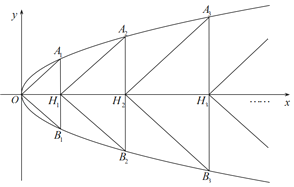
(1)求S1和S2的值;
(2)證明:n≤sn≤n2.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在![]() 上的函數
上的函數![]() 滿足
滿足![]() ,且
,且![]() ,則下列說法正確的有( )
,則下列說法正確的有( )
(1)若函數![]() ,則函數
,則函數![]() 是奇函數;
是奇函數;
(2)![]() ;
;
(3)設函數![]() ,則函數
,則函數![]() 的圖象經過點
的圖象經過點![]() ;
;
(4)設![]() ,若數列
,若數列![]() 是等比數列,則
是等比數列,則![]() .
.
A.(2)(3)(4)B.(1)(3)(4)C.(1)(3)D.(1)(2)(3)(4)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學棋藝協會定期舉辦“以棋會友”的競賽活動,分別包括“中國象棋”、“圍棋”、“五子棋”、“國際象棋”四種比賽,每位協會會員必須參加其中的兩種棋類比賽,且各隊員之間參加比賽相互獨立;已知甲同學必選“中國象棋”,不選“國際象棋”,乙同學從四種比賽中任選兩種參與.
(1)求甲參加圍棋比賽的概率;
(2)求甲、乙兩人參與的兩種比賽都不同的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com