
某地為迎接2014年索契冬奧會,舉行了一場奧運選拔賽,其中甲、乙兩名運動員為爭取最后一個參賽名額進行的7輪比賽,其得分情況如莖葉圖所示:
(1)若從甲運動員的不低于80且不高于90的得分中任選3個,求其中與平均得分之差的絕對值不超過2的概率;
(2)若分別從甲、乙兩名運動員的每輪比賽不低于80且不高于90的得分中任選1個,求甲、乙兩名運動員得分之差的絕對值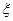 的分布列與期望.
的分布列與期望.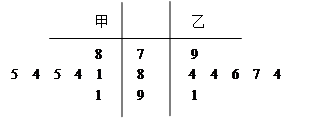
(1) ;(2)
;(2)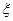 的分布列為:
的分布列為: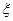
0 1 2 3 5 6 
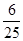
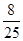
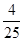
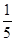
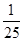
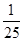
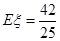 .
.
解析試題分析:(1)由題設要求,根據莖葉圖寫出甲的所有成績,計算出平均成績,然后計數不低于80且不高于90的得分有5個,其中與平均分的差的絕對值不超過2的有4個,那么就可以很快計算出所要要求的概率;(2)從圖中可知符合要求的成績甲、乙各有5個,各取一個其差的絕對值可能為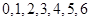 ,我們只要根據
,我們只要根據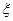 的各種情形,列出甲、乙的成績可能性,可一一求出相應的概率,列出其分布列,再根據公式求出其數學期望.
的各種情形,列出甲、乙的成績可能性,可一一求出相應的概率,列出其分布列,再根據公式求出其數學期望.
(1)由莖葉圖可知,甲運動員七輪比賽的得分情況為:78,81,84,85,84,85,91.
所以甲每輪比賽的平均得分為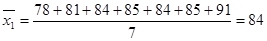
甲運動員每輪比賽得分中不低于80且不高于90的得分共有5個,
分別為81,84,85,84,85,其中81分與平均得分的絕對值大于2,
所求概率 4分
4分
(2)設甲、乙兩名運動員的得分分別為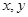 ,則得分之差的絕對值為
,則得分之差的絕對值為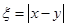 .
.
由莖葉圖可知,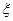 的可能取值為0,1,2,3,5,6.
的可能取值為0,1,2,3,5,6.
當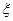 =0時,
=0時,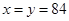 ,故
,故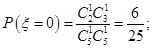
當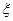 =1時,
=1時,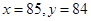 或
或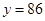 ,故
,故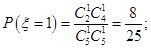
當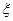 =2時,
=2時,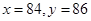 或
或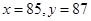 ,故
,故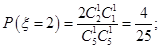
當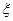 =3時,
=3時, 或
或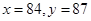 ,故
,故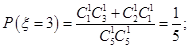
當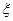 =5時,
=5時,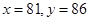 ,故
,故
當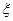 =6時,
=6時,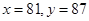 ,故
,故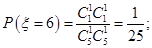 所以
所以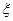 的分布列為:
的分布列為: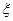
0 1 2 3 5 6 
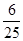
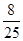
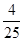
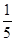
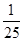
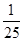
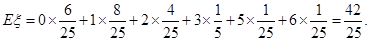 --12分
--12分
考點:(1)古典概型;(2)隨機變量的概率分布列與數學期望.


科目:高中數學 來源: 題型:解答題
從某企業生產的某種產品中抽取100件,測量這些產品的一項質量指標值,由測量表得如下頻數分布表:
| 質量指標值分組 | [75,85) | [85,95) | [95,105) | [105,115) | [115,125) |
| 頻數 | 6 | 26 | 38 | 22 | 8 |

查看答案和解析>>
科目:高中數學 來源: 題型:解答題
為調查民營企業的經營狀況,某統計機構用分層抽樣的方法從A、B、C三個城市中,抽取若干個民營企業組成樣本進行深入研究,有關數據見下表:(單位:個)
| 城市 | 民營企業數量 | 抽取數量 |
| A |  | 4 |
| B | 28 |  |
| C | 84 | 6 |
 、
、 的值;
的值;查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校為了解高一期末數學考試的情況,從高一的所有學生數學試卷中隨機抽取 份試卷進行成績分析,得到數學成績頻率分布直方圖(如圖所示),其中成績在
份試卷進行成績分析,得到數學成績頻率分布直方圖(如圖所示),其中成績在 的學生人數為6.
的學生人數為6.
(1)估計所抽取的數學成績的眾數;
(2)用分層抽樣的方法在成績為 和
和 這兩組中共抽取5個學生,并從這5個學生中任取2人進行點評,求分數在
這兩組中共抽取5個學生,并從這5個學生中任取2人進行點評,求分數在 恰有1人的概率.
恰有1人的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
(2014·泰安模擬)某中學為研究學生的身體素質與課外體育鍛煉時間的關系,對400名高一學生的一周課外體育鍛煉時間進行調查,結果如下表所示:
| 鍛煉時間 (分鐘) | [0,20) | [20,40) | [40,60) | [60,80) | [80,100) | [100,120) |
| 人數 | 40 | 60 | 80 | 100 | 80 | 40 |
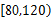 分鐘內的學生應抽取多少人?
分鐘內的學生應抽取多少人?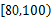 分鐘內的概率.
分鐘內的概率. 查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某單位N名員工參加“社區低碳你我他”活動,他們的年齡在25歲至50歲之間。按年齡分組:第1組 ,第2組
,第2組 ,第3組
,第3組 ,第4組
,第4組 ,第5組
,第5組 ,由統計的數據得到的頻率分布直方圖如圖所示,在其右面的表是年齡的頻率分布表。
,由統計的數據得到的頻率分布直方圖如圖所示,在其右面的表是年齡的頻率分布表。
(1)求正整數a,b,N的值;
(2)現要從年齡較小的第1,2,3組中用分層抽樣的方法抽取6人,則年齡在第1,2,3組中抽取的人數分別是多少?
(3)在(2)的條件下,從這6人中隨機抽取2人參加社區宣傳交流活動,求恰有1 人在第3組的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
從天氣網查詢到邯鄲歷史天氣統計(2011-01-01到2014-03-01)資料如下: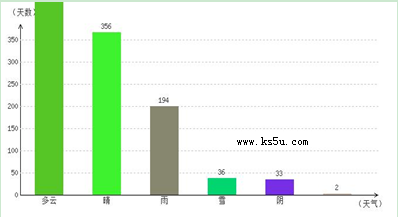
自2011-01-01到2014-03-01,邯鄲共出現:多云 天,晴
天,晴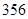 天,雨
天,雨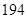 天,雪
天,雪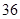 天,陰
天,陰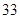 天,其它2天,合計天數為:
天,其它2天,合計天數為: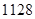 天.
天.
本市朱先生在雨雪天的情況下,分別以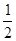 的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為
的概率乘公交或打出租的方式上班(每天一次,且交通方式僅選一種),每天交通費用相應為 元或
元或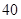 元;在非雨雪天的情況下,他以
元;在非雨雪天的情況下,他以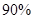 的概率騎自行車上班,每天交通費用
的概率騎自行車上班,每天交通費用 元;另外以
元;另外以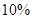 的概率打出租上班,每天交通費用
的概率打出租上班,每天交通費用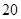 元.(以頻率代替概率,保留兩位小數. 參考數據:
元.(以頻率代替概率,保留兩位小數. 參考數據: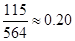 )
)
(1)求他某天打出租上班的概率;
(2)將他每天上班所需的費用記為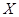 (單位:元),求
(單位:元),求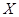 的分布列及數學期望.
的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高三年級一次數學考試后,為了解學生的數學學習情況,隨機抽取 名學生的數學成績,制成表所示的頻率分布表.
名學生的數學成績,制成表所示的頻率分布表.
| 組號 | 分組 | 頻數 | 頻率 |
| 第一組 |  |  |  |
| 第二組 |  |  |  |
| 第三組 |  |  |  |
| 第四組 |  | 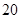 |  |
| 第五組 |  |  |  |
| 合計 |  |  | |
 、
、 、
、 的值;
的值; 名學生,并在這
名學生,并在這 名學生中隨機抽取
名學生中隨機抽取 名學生與張老師面談,求第三組中至少有
名學生與張老師面談,求第三組中至少有 名學生與張老師面談的概率
名學生與張老師面談的概率查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
該興趣小組確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗。
(1)求選取的2組數據恰好是相鄰兩個月的概率;
(2)若選取的是1月與6月的兩組數據,請根據2至5月份的數據,求出y關于x的線
性回歸方程 ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com