
某興趣小組欲研究晝夜溫差大小與患感冒人數多少之間的關系,他們分別到氣象局與某醫院抄錄了1至6月份每月10號的晝夜溫差情況與因患感冒而就診的人數,得到如下資料:
該興趣小組確定的研究方案是:先從這六組數據中選取2組,用剩下的4組數據求線性回歸方程,再用被選取的2組數據進行檢驗。
(1)求選取的2組數據恰好是相鄰兩個月的概率;
(2)若選取的是1月與6月的兩組數據,請根據2至5月份的數據,求出y關于x的線
性回歸方程 ;
;
(3)若由線性回歸方程得到的估計數據與所選出的檢驗數據的誤差均不超過2人,則認為得到的線性回歸方程是理想的,試問該小組所得線性回歸方程是否理想?
(1)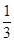 ;(2)
;(2)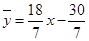 ;(3)理想.
;(3)理想.
解析試題分析:(1)本題是一個古典概型,試驗發生包含的事件是從6組數據中選取2組數據共有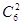 種情況,滿足條件的事件是抽到相鄰兩個月的數據的情況有5種,根據古典概型的概率公式得到結果.
種情況,滿足條件的事件是抽到相鄰兩個月的數據的情況有5種,根據古典概型的概率公式得到結果.
(2)根據所給的數據,求出 的平均數,根據求線性回歸方程系數的方法,求出系數
的平均數,根據求線性回歸方程系數的方法,求出系數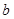 ,把
,把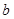 和
和 的平均數,代入求
的平均數,代入求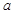 的公式,做出a的值,寫出線性回歸方程.
的公式,做出a的值,寫出線性回歸方程.
(3)根據所求的線性回歸方程,預報當自變量為10和6時的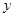 的值,把預報的值同原來表中所給的10和6對應的值做差,差的絕對值不超過2,得到線性回歸方程理想.
的值,把預報的值同原來表中所給的10和6對應的值做差,差的絕對值不超過2,得到線性回歸方程理想.
試題解析:解 (1)設抽到相鄰兩個月的數據為事件A因為從6組數據中選取2組數據共有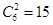 中情況,每種情況都是等可能出現的其中,抽到相鄰兩個月的數據的情況有5種
中情況,每種情況都是等可能出現的其中,抽到相鄰兩個月的數據的情況有5種
所以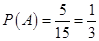
(2)由數據求得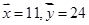
由公式求得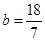
再由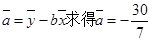
所以y關于x的線性回歸方程為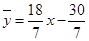
(3)當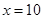 時,
時,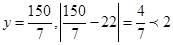
同樣,當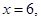 時,
時,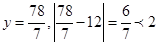
所以,該小組所得線性回歸方程是理想的。
考點:1.古典概型的概率;2.求線性回歸方程.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:解答題
某地為迎接2014年索契冬奧會,舉行了一場奧運選拔賽,其中甲、乙兩名運動員為爭取最后一個參賽名額進行的7輪比賽,其得分情況如莖葉圖所示:
(1)若從甲運動員的不低于80且不高于90的得分中任選3個,求其中與平均得分之差的絕對值不超過2的概率;
(2)若分別從甲、乙兩名運動員的每輪比賽不低于80且不高于90的得分中任選1個,求甲、乙兩名運動員得分之差的絕對值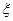 的分布列與期望.
的分布列與期望.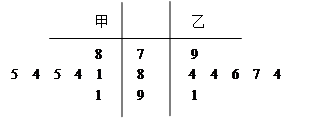
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在調查男女同學是否喜愛籃球的情況中,已知男同學喜愛籃球的為28人,不喜愛籃球的也是28人,而女同學喜愛籃球的為28人,不喜愛籃球的為56人,
(1)根據以上數據建立一個2×2的列聯表;
(2)試判斷是否喜愛籃球與性別有關?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某班共有學生40人,將以此數學考試成績(單位:分)繪制成頻率分布直方圖,如圖所示.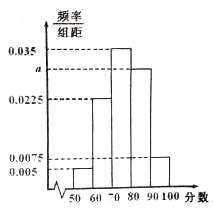
(1)請根據圖中所給的數據,求a的值;
(2)從成績在[50,70)內的學生中隨機選3名學生,求這3名學生的成績都在[60,70)內的概率;
(3)為了了解學生這次考試的失分情況,從成績在[50,70)內的學生中隨機選取3人的成績進行分析,用X表示所選學生成績在[60,70)內的人數,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某學校制定學校發展規劃時,對現有教師進行年齡狀況和接受教育程度(學歷)的調查,其結果(人數分布)如表:
| 學歷 | 35歲以下 | 35至50歲 | 50歲以上 |
| 本科 | 80 | 30 | 20 |
| 研究生 | x | 20 | y |
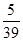 ,求x、y的值.
,求x、y的值.查看答案和解析>>
科目:高中數學 來源: 題型:解答題
根據我國發布的《環境空氣質量指數 技術規定》 (試行),
技術規定》 (試行), 共分為六級:
共分為六級: 為優,
為優, 為良,
為良, 為輕度污染,
為輕度污染, 為中度污染,
為中度污染, ,
, 均為重度污染,
均為重度污染, 及以上為嚴重污染.某市2013年11月份
及以上為嚴重污染.某市2013年11月份 天的
天的 的頻率分布直方圖如圖所示:
的頻率分布直方圖如圖所示:
(1)該市11月份環境空氣質量優或良的共有多少天?
(2)若采用分層抽樣方法從 天中抽取
天中抽取 天進行市民戶外晨練人數調查,則中度污染被抽到的天數共有多少天?
天進行市民戶外晨練人數調查,則中度污染被抽到的天數共有多少天?
(3)空氣質量指數低于 時市民適宜戶外晨練,若市民王先生決定某天早晨進行戶外晨練,則他當天適宜戶外晨練的概率是多少?
時市民適宜戶外晨練,若市民王先生決定某天早晨進行戶外晨練,則他當天適宜戶外晨練的概率是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某校高一(1)班的一次數學測試成績的莖葉圖和頻率分布直方圖都受到不同程度的污損,可見部分如下圖.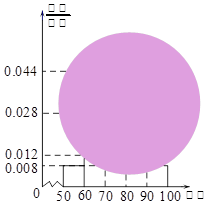

(1)求分數在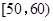 的頻率及全班人數;
的頻率及全班人數;
(2)求分數在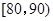 之間的頻數,并計算頻率分布直方圖中
之間的頻數,并計算頻率分布直方圖中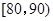 間矩形的高;
間矩形的高;
(3)若要從分數在 之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在
之間的試卷中任取兩份分析學生失分情況,求在抽取的試卷中,至少有一份分數在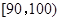 之間的概率.
之間的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖是總體的一個樣本頻率分布直方圖,且在區間[15,18)內的頻數為8.
(1)求樣本容量;
(2)若在[12,15)內的小矩形的面積為0.06,
①求樣本在[12,15)內的頻數;
②求樣本在[18,33)內的頻率。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
在某次測驗中,有6位同學的平均成績為75分.用 表示編號為
表示編號為 (
( )的同學所得成績,且前5位同學的成績如下:70,76,72,70,72.
)的同學所得成績,且前5位同學的成績如下:70,76,72,70,72.
(1)求第6位同學的成績 ,及這6位同學成績的標準差
,及這6位同學成績的標準差 ;
;
(2)從前5位同學中,隨機地選2位同學,求恰有1位同學成績在區間(68,75)中的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com