解:(1)當x<1時,f(x)=-x
3+x
2+bx+c,∴f′(x)=-3x
2+2x+b
∵函數在點(-1,f(-1))處的切線的斜率是-5,∴f′(-1)=-5
∴-3-2+b=-5,∴b=0
∵f(0)=0,∴c=0
∴b=0,c=0
(2)當x<1時,f(x)=-x
3+x
2,∴f′(x)=-3x
2+2x
令f′(x)=0有-3x
2+2x=0,∴x=0或x=

令f′(x)>0,可得0<x<

;令f′(x)<0,∵-1≤x≤1,∴-1≤x<0或
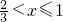
∴函數在-1,0,

,1出取得最值
∵f(-1)=2,f(0)=0,f(

)=

,f(1)=0
∴函數f(x)在區間[-1,1]上的最小值為0;
(3)設P(x
1,f(x
1)),因為PQ中點在y軸上,所以Q(-x
1,f(-x
1)),
∵OP⊥OQ,∴
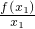
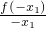
=-1
①當x
1=1時,f(x
1)=0;當x
1=-1時,f(-x
1)=0,∴
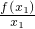
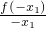
≠-1;
②當-1<x
1<1時,f(x
1)=
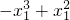
,f(-x
1)=
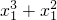
,代入
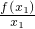
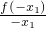
=-1,可得
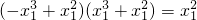
,∴
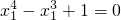
,無解;
③當x
1>1時,f(x
1)=alnx
1,f(-x
1)=
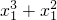
,代入
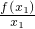
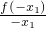
=-1,可得
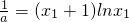
;
設g(x
1)=(x
1+1)lnx
1(x
1>1),∴g′(x
1)=lnx
1+
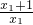
>0,∴g(x
1)是增函數
∵g(1)=0,∴g(x
1)值域是(0,+∞)
∴對任意給定的正實數a,
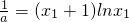
恒有解,滿足條件
④由P,Q橫坐標的對稱性可得,當x
1<-1時,f(x
1)=
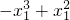
,f(-x
1)=aln(-x
1),
代入
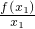
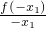
=-1,可得
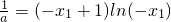
設h(x
1)=(-x
1+1)ln(-x
1)(x
1<-1),∴h′(x
1)=-ln(-x
1)-
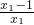
<0,∴h(x
1)是減函數
∵h(-1)=0,∴h(x
1)值域是(0,+∞)
∴對任意給定的正實數a,
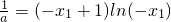
恒有解,滿足條件
綜上所述,滿足條件的點P的橫坐標的取值范圍為(-∞,-1)∪(1,+∞).
分析:(1)求導數,根據函數在點(-1,f(-1))處的切線的斜率是-5,圖象過坐標原點,即可求得實數b,c的值;
(2)當x<1時,f(x)=-x
3+x
2,求導函數,確定函數的單調性,計算函數值,從而可得函數f(x)在區間[-1,1]上的最小值;
(3)設P(x
1,f(x
1)),因為PQ中點在y軸上,所以Q(-x
1,f(-x
1)),根據OP⊥OQ,可得
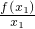
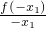
=-1,分類討論,確定函數的解析式,利用
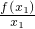
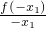
=-1,即可求得結論.
點評:本題考查導數知識的運用,考查函數的單調性與最值,考查分類討論的數學思想,考查學生分析解決問題的能力,正確分類,靈活運用導數是關鍵.

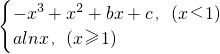 和圖象過坐標原點O,且在點(-1,f(-1))處的切線的斜率是-5.
和圖象過坐標原點O,且在點(-1,f(-1))處的切線的斜率是-5.
 ;令f′(x)<0,∵-1≤x≤1,∴-1≤x<0或
;令f′(x)<0,∵-1≤x≤1,∴-1≤x<0或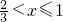
 ,1出取得最值
,1出取得最值 )=
)= ,f(1)=0
,f(1)=0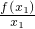
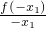 =-1
=-1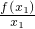
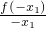 ≠-1;
≠-1;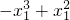 ,f(-x1)=
,f(-x1)=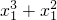 ,代入
,代入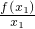
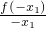 =-1,可得
=-1,可得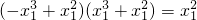 ,∴
,∴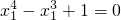 ,無解;
,無解;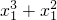 ,代入
,代入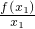
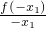 =-1,可得
=-1,可得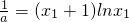 ;
;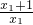 >0,∴g(x1)是增函數
>0,∴g(x1)是增函數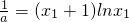 恒有解,滿足條件
恒有解,滿足條件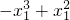 ,f(-x1)=aln(-x1),
,f(-x1)=aln(-x1),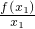
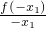 =-1,可得
=-1,可得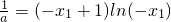
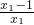 <0,∴h(x1)是減函數
<0,∴h(x1)是減函數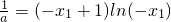 恒有解,滿足條件
恒有解,滿足條件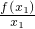
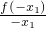 =-1,分類討論,確定函數的解析式,利用
=-1,分類討論,確定函數的解析式,利用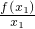
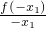 =-1,即可求得結論.
=-1,即可求得結論.

 口算能手系列答案
口算能手系列答案