
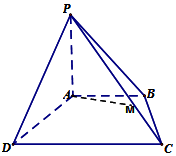
 四棱錐P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.
四棱錐P-ABCD中,PA⊥底面ABCD,且PA=AB=AD=$\frac{1}{2}$CD,AB∥CD,∠ADC=90°.分析 (1)取Q為側棱PC中點,取PD的中點E,連AE、EQ、BQ,∵Q、E分別為PC、PD的中點,證明BQ∥AE.只需證AE⊥平面PCD,通過證明PA⊥CD.AD⊥CD,推出CD⊥平面PAD.得到CD⊥AE,AE⊥PD,推出AE⊥平面PCD.如何證明平面PBC⊥平面PCD.
(2)建立空間直角坐標系,設PA=AB=AD=1,CD=2,求出相關點的坐標,平面PBC的法向量,求出$\overrightarrow{AM}$=($\frac{2}{3}$,$\frac{4}{3}$,$\frac{1}{3}$).設所求線面角為θ,利用數量積求解即可.
解答 證明:(1)取Q為側棱PC中點
如圖,取PD的中點E,連AE、EQ、BQ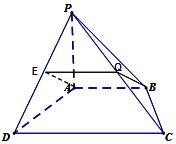
∵Q、E分別為PC、PD的中點,∴EQ為△PCD的中位線,
∴EQ∥AB且EQ=AB,
∴四邊形ABQE為平行四邊形,則BQ∥AE.
只需證AE⊥平面PCD
∵PA⊥底面ABCD,∴PA⊥CD.
又∵AD⊥CD,PA∩AD=A,∴CD⊥平面PAD.
∵AE?平面PAD,∴CD⊥AE,
∵PA=AD,E為PD中點,∴AE⊥PD?
∵CD∩PD=D,∴由??得AE⊥平面PCD.
∵BQ∥AE,∴BQ⊥平面PCD.
∵BQ?平面PBC,∴平面PBC⊥平面PCD.
(2)如圖所示建立空間直角坐標系,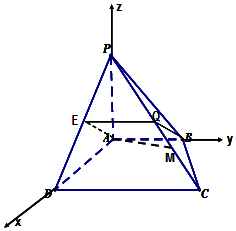
設PA=AB=AD=1,CD=2,則A(0,0,0),B(0,1,0),C(1,2,0),P(0,0,1)
則$\overrightarrow{PB}$=(0,1,-1),$\overrightarrow{BC}$=(1,1,0).
設平面PBC的法向量為$\overrightarrow n=(x,y,z)$,則
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{PB}=0}\\{\overrightarrow{n}•\overrightarrow{BC}=0}\end{array}\right.$即$\left\{\begin{array}{l}{y-z=0}\\{x+y=0}\end{array}\right.$,不妨令x=-1,∴$\overrightarrow{n}$=(-1,1,1).
由$\overrightarrow{PM}$=$\frac{2}{3}$$\overrightarrow{PC}$,有M($\frac{2}{3}$,$\frac{4}{3}$,$\frac{1}{3}$),∴$\overrightarrow{AM}$=($\frac{2}{3}$,$\frac{4}{3}$,$\frac{1}{3}$).
設所求線面角為θ,則sinθ=$\frac{|\overrightarrow{AM}•\overrightarrow{n}|}{|\overrightarrow{AM}||\overrightarrow{n}|}$=$\frac{1}{\sqrt{\frac{21}{9}}•\sqrt{3}}$=$\frac{\sqrt{7}}{7}$.
∴所求線面角的正弦值為$\frac{{\sqrt{7}}}{7}$.
點評 本題考查直線與平面所成角的求法,平面與平面垂直的判定定理以及直線與平面垂直的判定定理的應用,考查空間想象能力、邏輯推理能力以及計算能力.


科目:高中數學 來源: 題型:選擇題
| A. | A=B=C | B. | A⊆C | C. | A∩C=B | D. | B⊆A∩C |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
 (1)某簡單幾何體的三視圖中,正視圖、側視圖、俯視圖都是如圖所示的直角邊長為1的等腰直角三角形,求該幾何體的表面積和體積;
(1)某簡單幾何體的三視圖中,正視圖、側視圖、俯視圖都是如圖所示的直角邊長為1的等腰直角三角形,求該幾何體的表面積和體積;查看答案和解析>>
科目:高中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com