
【題目】在平面直角坐標系![]() 中,橢圓
中,橢圓![]() 的左、右焦點分別為
的左、右焦點分別為![]() ,離心率
,離心率![]() .過
.過![]() 的直線
的直線![]() 與橢圓
與橢圓![]() 相交于
相交于![]() 兩點,且
兩點,且![]() 的周長為
的周長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)若點![]() 位于第一象限,且
位于第一象限,且![]() ,求
,求![]() 的外接圓的方程.
的外接圓的方程.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】十二生肖是十二地支的形象化代表,即子(鼠)、丑(牛)、寅(虎)、卯(兔)、辰(龍)、巳(蛇)、午(馬)、未(羊)、申(猴)、酉(雞)、戌(狗)、亥(豬),每一個人的出生年份對應了十二種動物中的一種,即自己的屬相.現有印著六種不同生肖圖案(包含馬、羊)的毛絨娃娃各一個,小張同學的屬相為馬,小李同學的屬相為羊,現在這兩位同學從這六個毛絨娃娃中各隨機取一個(不放回),則這兩位同學都拿到自己屬相的毛絨娃娃的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐E-ABCD中,底面ABCD為正方形,![]() 平面CDE.已知
平面CDE.已知![]() ,
,![]() .
.
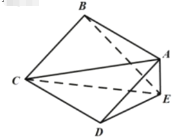
(1)證明:平面![]() 平面ABCD;
平面ABCD;
(2)求直線BE與平面ACE所成的角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 為坐標原點,點
為坐標原點,點![]() 和點
和點![]() ,動點
,動點![]() 滿足:
滿足:![]() .
.
(1)求動點![]() 的軌跡曲線
的軌跡曲線![]() 的方程并說明
的方程并說明![]() 是何種曲線;
是何種曲線;
(2)若拋物線![]() :
:![]() 的焦點
的焦點![]() 恰為曲線
恰為曲線![]() 的頂點,過點
的頂點,過點![]() 的直線
的直線![]() 與拋物線
與拋物線![]() 交于
交于![]() ,
,![]() 兩點,
兩點,![]() ,求直線
,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖①,在直角梯形中![]() ,
,![]() ,
,![]() ,
,![]() ,點
,點![]() 是
是![]() 邊的中點,將
邊的中點,將![]() 沿
沿![]() 折起,使平面
折起,使平面![]() 平面
平面![]() ,連接
,連接![]() ,
,![]() ,
,![]() ,得到如圖②所示的幾何體.
,得到如圖②所示的幾何體.
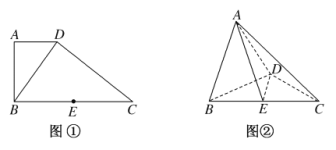
(1)求證:![]() 平面
平面![]() ;
;
(2)若![]() ,二面角
,二面角![]() 的平面角的正切值為
的平面角的正切值為![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】謝賓斯基三角形是一種分形,由波蘭數學家謝賓斯基在1915年提出,先作一個正三角形.挖去一個“中心三角形”(即以原三角形各邊的中點為頂點的三角形),然后在剩下的小三角形中又挖去一個“中心三角形”,我們用白色代表挖去的面積,那么黑三角形為剩下的面積(我們稱黑三角形為謝賓斯基三角形).向圖中第5個大正三角形中隨機撒512粒大小均勻的細小顆粒物,則落在白色區域的細小顆粒物的數量約是( )

A.256B.350C.162D.96
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓:![]() 的右焦點為
的右焦點為![]() 點的坐標為
點的坐標為![]() ,
,![]() 為坐標原點,
為坐標原點,![]() 是等腰直角三角形.
是等腰直角三角形.
(1)求橢圓![]() 的方程;
的方程;
(2)經過點![]() 作直線
作直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點,求
兩點,求![]() 面積的最大值;
面積的最大值;
(3)是否存在直線![]() 交橢圓于
交橢圓于![]() 兩點,使點
兩點,使點![]() 為
為![]() 的垂心(垂心:三角形三邊高線的交點)?若存在,求出直線
的垂心(垂心:三角形三邊高線的交點)?若存在,求出直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)當![]() 時.
時.
①求函數![]() 在
在![]() 處的切線方程;
處的切線方程;
②定義![]() 其中
其中![]() ,求
,求![]() ;
;
(2)當![]() 時,設
時,設![]() ,
,![]() (
(![]() 為自然對數的底數),若對任意給定的
為自然對數的底數),若對任意給定的![]() ,在
,在![]() 上總存在兩個不同的
上總存在兩個不同的![]() ,使得
,使得![]() 成立,求
成立,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com