
【題目】定義在![]() 上的函數
上的函數![]() ,
,![]() 單調遞增,
單調遞增,![]() ,若對任意
,若對任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,則稱
成立,則稱![]() 是
是![]() 在
在![]() 上的“追逐函數”.若
上的“追逐函數”.若![]() ,則下列四個命題:①
,則下列四個命題:①![]() 是
是![]() 在
在![]() 上的“追逐函數”;②若
上的“追逐函數”;②若![]() 是
是![]() 在
在![]() 上的“追逐函數”,則
上的“追逐函數”,則![]() ;③
;③![]() 是
是![]() 在
在![]() 上的“追逐函數”;④當
上的“追逐函數”;④當![]() 時,存在
時,存在![]() ,使得
,使得![]() 是
是![]() 在
在![]() 上的“追逐函數”.其中正確命題的個數為( )
上的“追逐函數”.其中正確命題的個數為( )
A. ①③B. ②④C. ①④D. ②③
【答案】B
【解析】
由題意,分析每一個選項,首先判斷單調性,以及![]() ,再假設是
,再假設是
“追逐函數”,利用題目已知的性質,看是否滿足,然后確定答案.
對于①,可得![]() ,
,![]() 在
在![]() 是遞增函數,
是遞增函數,![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“追逐函數”;則
上的“追逐函數”;則![]() 存在
存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,此時當k=100時,不存在
,此時當k=100時,不存在![]() ,故①錯誤;
,故①錯誤;
對于②,若![]() 是
是![]() 在
在![]() 上的“追逐函數”,此時
上的“追逐函數”,此時![]() ,解得
,解得
![]() ,當
,當![]() 時,
時,![]() ,
,![]() 在
在![]() 是遞增函數,若是“追逐函數”
是遞增函數,若是“追逐函數”
則![]() ,即
,即![]() ,
,
設函數![]()
即![]() ,則存在
,則存在![]() ,所以②正確;
,所以②正確;
對于③![]() ,
,![]() 在
在![]() 是遞增函數,
是遞增函數,![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“追逐函數”;則
上的“追逐函數”;則![]() 存在
存在![]() ,使得
,使得![]() 成立,即
成立,即![]() ,當k=4時,就不存在
,當k=4時,就不存在![]() ,故③錯誤;
,故③錯誤;
對于④,當t=m=1時,就成立,驗證如下:
![]() ,
,![]() 在
在![]() 是遞增函數,
是遞增函數,![]() ,若
,若![]() 是
是![]() 在
在![]() 上的“追逐函數”;則
上的“追逐函數”;則![]() 存在
存在![]() ,使得
,使得![]() 成立,
成立,
即![]() 此時
此時![]()
取![]()
即![]() ,故存在存在
,故存在存在![]() ,所以④正確;
,所以④正確;
故選B


 狀元坊全程突破導練測系列答案
狀元坊全程突破導練測系列答案科目:高中數學 來源: 題型:
【題目】已知數列{an}的前n項和為Sn,滿足Sn=2an-1(n∈N*),數列{bn}滿足nbn+1-(n+1)bn=n(n+1)(n∈N*),且b1=1.
(1)證明數列{![]() }為等差數列,并求數列{an}和{bn}的通項公式;
}為等差數列,并求數列{an}和{bn}的通項公式;
(2)若cn=(-1)n-1![]() ,求數列{cn}的前n項和T2n;
,求數列{cn}的前n項和T2n;
(3)若dn=an![]() ,數列{dn}的前n項和為Dn,對任意的n∈N*,都有Dn≤nSn-a,求實數a的取值范圍.
,數列{dn}的前n項和為Dn,對任意的n∈N*,都有Dn≤nSn-a,求實數a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種設備隨著使用年限的增加,每年的維護費相應增加.現對一批該設備進行調查,得到這批設備自購入使用之日起,前5年平均每臺設備每年的維護費用大致如表:
年份 |
|
|
|
|
|
維護費 |
|
|
|
|
|
(I)從這![]() 年中隨機抽取兩年,求平均每臺設備每年的維護費用至少有
年中隨機抽取兩年,求平均每臺設備每年的維護費用至少有![]() 年多于
年多于![]() 萬元的概率;
萬元的概率;
(II)求![]() 關于
關于![]() 的線性回歸方程;若該設備的價格是每臺
的線性回歸方程;若該設備的價格是每臺![]() 萬元,你認為應該使用滿五年換一次設備,還是應該使用滿八年換一次設備?并說明理由.
萬元,你認為應該使用滿五年換一次設備,還是應該使用滿八年換一次設備?并說明理由.
參考公式:用最小二乘法求線性回歸方程![]() 的系數公式:
的系數公式: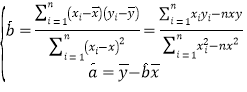
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將正方形ABCD沿對角線BD折成直二面角A-BD-C,有如下四個結論
①AC⊥BD;
②△ACD是等邊三角形;
③AB與平面BCD成60°的角;
④AB與CD所成的角是60°.
其中正確結論的序號是________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知離心率為2的雙曲線![]() 的一個焦點
的一個焦點![]() 到一條漸近線的距離為
到一條漸近線的距離為![]() .
.
(1)求雙曲線![]() 的方程;
的方程;
(2)設![]() 分別為
分別為![]() 的左右頂點,
的左右頂點,![]() 為
為![]() 異于
異于![]() 一點,直線
一點,直線![]() 與
與![]() 分別交
分別交![]() 軸于
軸于![]() 兩點,求證:以線段
兩點,求證:以線段![]() 為直徑的圓
為直徑的圓![]() 經過兩個定點.
經過兩個定點.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com