
【題目】已知函數f(x)=xlnx和g(x)=m(x2-1)(m∈R).
(1)m=1時,求方程f(x)=g(x)的實根;
(2)若對任意的x∈(1,+∞),函數y=g(x)的圖象總在函數y=f(x)圖象的上方,求m的取值范圍;
(3)求證: ![]() +
+![]() +…+
+…+![]() >ln(2n+1) (n∈N*).
>ln(2n+1) (n∈N*).
【答案】(1)見解析(2) ![]() .(3) 見解析
.(3) 見解析
【解析】試題分析:(1)代入![]() 時,
時, ![]() ,即
,即![]() ,整理方程得
,整理方程得![]() ,利用導數判斷函數的單調性為遞減函數,故最多有一個零點,而
,利用導數判斷函數的單調性為遞減函數,故最多有一個零點,而![]() ,故方程
,故方程![]() 有唯一的實根
有唯一的實根![]() ;(2)對于任意的
;(2)對于任意的![]() ,
, ![]() 恒成立,通過構造函數
恒成立,通過構造函數![]() ,利用導函數判斷函數的單調性,
,利用導函數判斷函數的單調性, ![]() ,通過討論
,通過討論![]() ,判斷是否符合題意;(3)由(2)知,當
,判斷是否符合題意;(3)由(2)知,當![]() 時,
時, ![]() 時,
時, ![]() 成立,結合題型,構造不妨令
成立,結合題型,構造不妨令![]() ,得出
,得出![]() ,利用累加可得結論.
,利用累加可得結論.
試題解析:(1) ![]() 時,
時, ![]() ,即
,即![]() ,而
,而![]() ,所以方程即為
,所以方程即為![]() .
.
令![]() ,則
,則![]() ,而
,而![]() ,故方程
,故方程![]() 有唯一的實根
有唯一的實根![]() .
.
(2)對于任意的![]() ,函數
,函數![]() 的圖象總在函數
的圖象總在函數![]() 圖象的上方,
圖象的上方,
即![]() ,
, ![]() ,即
,即![]() ,
,
設![]() ,即
,即![]() ,
, ![]() ,則
,則![]()
①若![]() ,則
,則![]() ,
, ![]() ,這與題設
,這與題設![]() 矛盾.
矛盾.
若![]() ,方程
,方程![]() 的判別式
的判別式![]() ,
,
當![]() ,即
,即![]() 時,
時, ![]()
∴![]() 在
在![]() 上單調遞減,
上單調遞減,
∴![]() ,即不等式成立.
,即不等式成立.
當![]() ,即
,即![]() 時,方程
時,方程![]() 有兩個實根,設兩根為
有兩個實根,設兩根為![]() ,
, ![]() 且
且![]() ,則
,則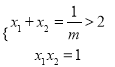
∴方程有兩個正實根且![]()
當![]() 時,
時, ![]() ,
, ![]() 單調遞增,
單調遞增, ![]() 與題設矛盾.
與題設矛盾.
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.
(3)證明 由(2)知,當![]() 時,
時, ![]() 時,
時, ![]() 成立.
成立.
不妨令![]()
∴![]() ,即
,即
![]()
∴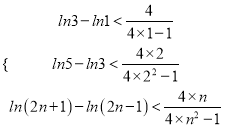 ,累加可得
,累加可得![]()


 靈星計算小達人系列答案
靈星計算小達人系列答案 孟建平錯題本系列答案
孟建平錯題本系列答案科目:高中數學 來源: 題型:
【題目】已知函數f(x)=x(1-![]() )是R上的偶函數.
)是R上的偶函數.
(1)對任意的x∈[1,2],不等式m·![]() ≥2x+1恒成立,求實數m的取值范圍.
≥2x+1恒成立,求實數m的取值范圍.
(2)令g(x)=1-![]() ,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
,設函數F(x)=g(4x-n)-g(2x+1-3)有零點,求實數n的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】直角三角形![]() 中,
中,![]() 是
是![]() 的中點,
的中點,![]() 是線段
是線段![]() 上一個動點,且
上一個動點,且![]() ,如圖所示,沿
,如圖所示,沿![]() 將
將![]() 翻折至
翻折至![]() ,使得平面
,使得平面![]() 平面
平面![]() .
.
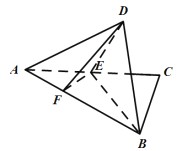
(1)當![]() 時,證明:
時,證明:![]() 平面
平面![]() ;
;
(2)是否存在![]() ,使得
,使得![]() 與平面
與平面![]() 所成的角的正弦值是
所成的角的正弦值是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點O,左焦點為F1(-1,0)的橢圓C的左頂點為A,上頂點為B,F1到直線AB的距離為![]() |OB|.
|OB|.
(1)求橢圓C的方程;
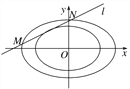
(2)如圖,若橢圓![]() ,橢圓
,橢圓![]() ,則稱橢圓C2是橢圓C1的λ倍相似橢圓.已知C2是橢圓C的3倍相似橢圓,若橢圓C的任意一條切線l交橢圓C2于兩點M、N,試求弦長|MN|的取值范圍.
,則稱橢圓C2是橢圓C1的λ倍相似橢圓.已知C2是橢圓C的3倍相似橢圓,若橢圓C的任意一條切線l交橢圓C2于兩點M、N,試求弦長|MN|的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,長方體![]() 中,
中, ![]() ,
, ![]() ,點
,點![]() ,
, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() ,
, ![]() 的中點,過點
的中點,過點![]() 的平面
的平面![]() 與平面
與平面![]() 平行,且與長方體的面相交,交線圍成一個幾何圖形.
平行,且與長方體的面相交,交線圍成一個幾何圖形.
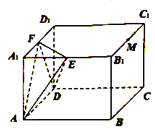
(1)在圖中畫出這個幾何圖形(說明畫法,不需要說明理由);
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
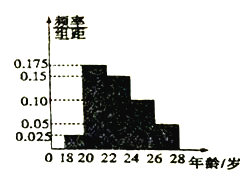
【題目】金磚國家領導人第九次會晤于2017年9月3日至5日在中國福建廈門市舉行,為了在金磚峰會期間為來到廈門的外國嘉賓提供服務,培訓部對兩千余名志愿者進行了集中培訓,為了檢驗培訓效果,現培訓部從兩千余名志愿者中隨機抽取100名,按年齡(單位:歲)分組:第1組![]() ,第2組
,第2組![]() ,第3組
,第3組![]() ,第4組
,第4組![]() ,第5組
,第5組![]() ,得到的頻率分布直方圖如圖所示.
,得到的頻率分布直方圖如圖所示.
(1)若從第3,4,5組中用分層抽樣的方法抽取6名志愿者前去機場參加接待外賓禮儀測試,則應從第3,4,5組中各抽取多少名志愿者?
(2)在(1)的條件下,若在第3,4組的志愿者中隨機抽取2名志愿者介紹接待外賓經驗感受,求第4組至少有1名志愿者被抽中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
: ![]() 的左、右焦點分別為
的左、右焦點分別為![]() 和
和![]() ,離心率是
,離心率是![]() ,直線
,直線![]() 過點
過點![]() 交橢圓于
交橢圓于![]() ,
, ![]() 兩點,當直線
兩點,當直線![]() 過點
過點![]() 時,
時, ![]() 的周長為
的周長為![]() .
.
(Ⅰ)求橢圓![]() 的標準方程;
的標準方程;
(Ⅱ)當直線![]() 繞點
繞點![]() 運動時,試求
運動時,試求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com