
閱讀下面材料:
根據兩角和與差的正弦公式,有
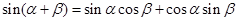 ------①
------①
 ------②
------②
由①+② 得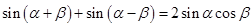 ------③
------③
令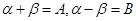 有
有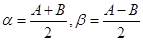
代入③得  .
.
(Ⅰ) 類比上述推理方法,根據兩角和與差的余弦公式,證明:
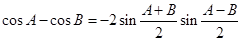 ;
;
(Ⅱ)若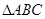 的三個內角
的三個內角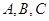 滿足
滿足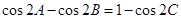 ,試判斷
,試判斷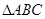 的形狀.
的形狀.
(提示:如果需要,也可以直接利用閱讀材料及(Ⅰ)中的結論)
(Ⅰ)證明見解析 (Ⅱ) 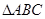 為直角三角形.
為直角三角形.
【解析】(1)通過觀察可知當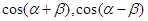 相減可得
相減可得 積,然后再令
積,然后再令 即可證明.
即可證明.
(2)根據二倍角化式可知,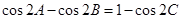
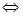
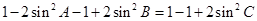
所以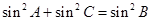 ,進而得到
,進而得到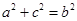 ,所以
,所以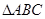 為直角三角形.
為直角三角形.
解法一:(Ⅰ)證明:因為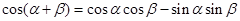 ,------①
,------①
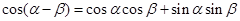 ,------②……………………………1分
,------②……………………………1分
①-② 得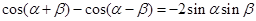 .------③…………………2分
.------③…………………2分
令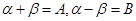 有
有 ,
,
代入③得 .……………5分
.……………5分
(Ⅱ)由二倍角公式,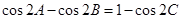 可化為
可化為
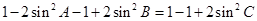 ,……………………………8分
,……………………………8分
所以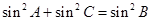 .……………………………………………9分
.……………………………………………9分
設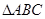 的三個內角A,B,C所對的邊分別為
的三個內角A,B,C所對的邊分別為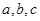 ,
,
由正弦定理可得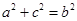 .…………………………………………11分
.…………………………………………11分
根據勾股定理的逆定理知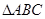 為直角三角形.…………………………12分
為直角三角形.…………………………12分
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的結論和二倍角公式,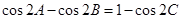 可化為
可化為
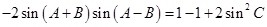 ,……………………8分
,……………………8分
因為A,B,C為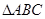 的內角,所以
的內角,所以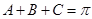 ,
,
所以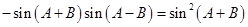 .
.
又因為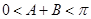 ,所以
,所以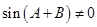 ,
,
所以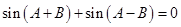 .
.
從而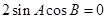 .……………………………………………9分
.……………………………………………9分
又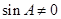 ,所以
,所以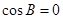 ,故
,故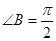 .…………………………………11分
.…………………………………11分
所以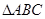 為直角三角形.
為直角三角形.


 七星圖書口算速算天天練系列答案
七星圖書口算速算天天練系列答案 初中學業考試導與練系列答案
初中學業考試導與練系列答案科目:高中數學 來源: 題型:閱讀理解
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:閱讀理解
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:閱讀理解
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:閱讀理解
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
| A+B |
| 2 |
| A-B |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年福建省高三5月月考文科數學試卷(解析版) 題型:解答題
閱讀下面材料:
根據兩角和與差的正弦公式,有
 ------①
------①
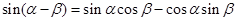 ------②
------②
由①+② 得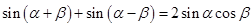 ------③
------③
令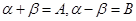 有
有
代入③得
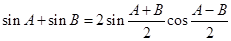 .
.
(Ⅰ)類比上述推證方法,根據兩角和與差的余弦公式,證明:
 ;
;
(Ⅱ)若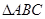 的三個內角
的三個內角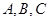 滿足
滿足 ,試判斷
,試判斷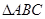 的形狀.
的形狀.
(提示:如果需要,也可以直接利用閱讀材料及(Ⅰ)中的結論)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com