
【題目】已知 a∈R,函數 f(x)=a﹣ ![]() .
.
(1)證明:f(x)在(﹣∞,+∞)上單調遞增;
(2)若f(x)為奇函數,求:
①a的值;
②f(x)的值域.
【答案】
(1)證明:證法一:設x1<x2,
則 ![]() ,
, ![]() ,
, ![]()
則f(x1)﹣f(x2)=(a﹣ ![]() )﹣(a﹣
)﹣(a﹣ ![]() )=
)= ![]() <0.
<0.
∴f(x1)﹣f(x2)<0,
∴f(x1)<f(x2),
故f(x)在(﹣∞,+∞)上單調遞增;
證法二:∵函數 f(x)=a﹣ ![]() .
.
∴f′(x)= ![]() ,
,
∵f′(x)>0恒成立,
故f(x)在(﹣∞,+∞)上單調遞增
(2)證明:①若f(x)為奇函數,
則 f(0)=a﹣ ![]() =0,
=0,
解得:a= ![]() ,
,
②f(x)= ![]() ﹣
﹣ ![]() ,
,
∵2x+1>1,
∴0< ![]() <1,
<1,
故﹣ ![]() <f(x)<
<f(x)< ![]() ,
,
故函數的值域為:(﹣ ![]() ,
, ![]() )
)
【解析】(1)證法一:設x1<x2 , 作差比較作差可得f(x1)<f(x2),根據函數單調性的定義,可得:f(x)在(﹣∞,+∞)上單調遞增;
證法二:求導,根據f′(x)>0恒成立,可得:f(x)在(﹣∞,+∞)上單調遞增.(2)①若f(x)為奇函數,則 f(0)=0,解得a的值;
②根據①可得函數的解析式,進而可得f(x)的值域.
【考點精析】通過靈活運用函數的值域和函數單調性的判斷方法,掌握求函數值域的方法和求函數最值的常用方法基本上是相同的.事實上,如果在函數的值域中存在一個最小(大)數,這個數就是函數的最小(大)值.因此求函數的最值與值域,其實質是相同的;單調性的判定法:①設x1,x2是所研究區間內任兩個自變量,且x1<x2;②判定f(x1)與f(x2)的大小;③作差比較或作商比較即可以解答此題.


科目:高中數學 來源: 題型:
【題目】《萊因德紙草書》(Rhind Papyrus)是世界上最古老的數學著作之一.書中有一道這樣的題目:把100個面包分給5個人,使每個人所得成等差數列,且使較大的三份之和的 ![]() 是較小的兩份之和,問最小一份為( )
是較小的兩份之和,問最小一份為( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【選修4-4:坐標系與參數方程】
在直角坐標系![]() 中圓C的參數方程為
中圓C的參數方程為![]() (
(![]() 為參數),以原點O為極點,
為參數),以原點O為極點, ![]() 軸的非負半軸為極軸建立極坐標系,直線
軸的非負半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]()
(1)求圓C的直角坐標方程及其圓心C的直角坐標;
(2)設直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的面積.
的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,空氣質量成為人們越來越關注的話題,空氣質量指數(![]() ,簡稱
,簡稱![]() )是定量描述空氣質量狀況的指數,空氣質量按照
)是定量描述空氣質量狀況的指數,空氣質量按照![]() 大小分為六級,
大小分為六級, ![]() 為優;
為優; ![]() 為良;
為良; ![]() 為輕度污染;
為輕度污染; ![]() 為中度污染;
為中度污染; ![]() 為重度污染;大于300為嚴重污染.環保部門記錄了2017年某月哈爾濱市10天的
為重度污染;大于300為嚴重污染.環保部門記錄了2017年某月哈爾濱市10天的![]() 的莖葉圖如下:
的莖葉圖如下:
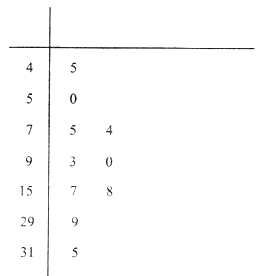
(1)利用該樣本估計該地本月空氣質量優良(![]() )的天數;(按這個月總共30天計算)
)的天數;(按這個月總共30天計算)
(2)現工作人員從這10天中空氣質量為優良的日子里隨機抽取2天進行某項研究,求抽取的2天中至少有一天空氣質量是優的概率;
(3)將頻率視為概率,從本月中隨機抽取3天,記空氣質量優良的天數為![]() ,求
,求![]() 的概率分布列和數學期望.
的概率分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓![]() ,定義橢圓的“伴隨圓”方程為
,定義橢圓的“伴隨圓”方程為![]() ;若拋物線
;若拋物線![]() 的焦點與橢圓C的一個短軸端點重合,且橢圓C的離心率為
的焦點與橢圓C的一個短軸端點重合,且橢圓C的離心率為![]() .
.
(1)求橢圓C的方程和“伴隨圓”E的方程;
(2)過“伴隨圓”E上任意一點P作橢圓C的兩條切線PA,PB,A,B為切點,延長PA與“伴隨圓”E交于點Q,O為坐標原點.
(i)證明:PA⊥PB;
(ii)若直線OP,OQ的斜率存在,設其分別為![]() ,試判斷
,試判斷![]() 是否為定值,若是, 求出該值;若不是,請說明理由.
是否為定值,若是, 求出該值;若不是,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,曲線
,曲線![]() 在點
在點![]() 處的切線與直線
處的切線與直線![]() 垂直(其中
垂直(其中![]() 為自然對數的底數).
為自然對數的底數).
(1)求![]() 的解析式及單調遞減區間;
的解析式及單調遞減區間;
(2)是否存在常數![]() ,使得對于定義域內的任意
,使得對于定義域內的任意![]() ,
, ![]() 恒成立,若存在,求出
恒成立,若存在,求出![]() 的值;若不存在,請說明理由.
的值;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中裝有圍棋黑色和白色棋子共7枚,從中任取2枚棋子都是白色的概率為![]() . 現有甲、乙兩人從袋中輪流摸取一枚棋子.甲先摸,乙后取,然后甲再取,……,取后均不放回,直到有一人取到白棋即終止. 每枚棋子在每一次被摸出的機會都是等可能的.用
. 現有甲、乙兩人從袋中輪流摸取一枚棋子.甲先摸,乙后取,然后甲再取,……,取后均不放回,直到有一人取到白棋即終止. 每枚棋子在每一次被摸出的機會都是等可能的.用![]() 表示取棋子終止時所需的取棋子的次數.
表示取棋子終止時所需的取棋子的次數.
(1)求隨機變量![]() 的概率分布列和數學期望
的概率分布列和數學期望![]() ;
;
(2)求甲取到白棋的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com