
【題目】如圖所示,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,
, ![]()
![]() 是線段
是線段![]() 的中垂線,
的中垂線,![]()
![]() ,
,![]() 為線段
為線段![]() 上的點.
上的點.

(Ⅰ)證明:平面![]() 平面
平面![]() ;
;
(Ⅱ)若![]() 為
為![]() 的中點,求異面直線
的中點,求異面直線![]() 與
與![]() 所成角的正切值;
所成角的正切值;
(Ⅲ)求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出下列四個結論:
,給出下列四個結論:
①函數![]() 的最小正周期是
的最小正周期是![]()
②函數![]() 在區間
在區間![]() 上是減函數
上是減函數
③函數![]() 的圖像關于點
的圖像關于點![]() 對稱
對稱
④函數![]() 的圖像可由函數
的圖像可由函數![]() 的圖像向左平移
的圖像向左平移![]() 個單位得到
個單位得到
其中正確結論的個數是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某小區為了調查居民的生活水平,隨機從小區住戶中抽取![]() 個家庭,得到數據如下:
個家庭,得到數據如下:
家庭編號 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x(千元) | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y(千元) | 4 | 5 | 6 | 8 | 8 | 11 |
參考公式:回歸直線的方程是:![]() ,其中,
,其中,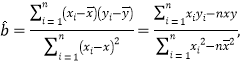
![]() .
.
(1)據題中數據,求月支出![]() (千元)關于月收入
(千元)關于月收入![]() (千元)的線性回歸方程(保留一位小數);
(千元)的線性回歸方程(保留一位小數);
(2)從這![]() 個家庭中隨機抽取
個家庭中隨機抽取![]() 個,求月支出都少于
個,求月支出都少于![]() 萬元的概率.
萬元的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為響應黨中央號召,學校以“我們都是追夢人”為主題舉行知識競賽。現有10道題,其中6道甲類題,4道乙類題,王同學從中任取3道題解答.
(Ⅰ)求王同學至少取到2道乙類題的概率;
(Ⅱ)如果王同學答對每道甲類題的概率都是![]() ,答對每道乙類題的概率都是
,答對每道乙類題的概率都是![]() ,且各題答對與否相互獨立,已知王同學恰好選中2道甲類題,1道乙類題,用
,且各題答對與否相互獨立,已知王同學恰好選中2道甲類題,1道乙類題,用![]() 表示王同學答對題的個數,求隨機變量
表示王同學答對題的個數,求隨機變量![]() 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產并銷售某高科技產品,已知每年生產該產品的固定成本是800萬元,生產成本e(單位;萬元)與生產的產品件數x(單位:萬件)的平方成正比;該產品單價p(單位:元)與生產的產品件數x滿足![]() (b為常數),已知當該產品的單價為300元時,生產成本是1800萬元,當單價為320元時,生產成本是200萬元,且工廠生產的產品都可以銷售完.
(b為常數),已知當該產品的單價為300元時,生產成本是1800萬元,當單價為320元時,生產成本是200萬元,且工廠生產的產品都可以銷售完.
(1)每年生產該產品多少萬件時,平均成本最低,最低為多少?
(2)若該工廠希望年利潤不低于8200萬元,則每年大約應該生產多少萬件該產品?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知球的半徑為4,球面被互相垂直的兩個平面所截,得到的兩個圓的公共弦長為2![]() .若球心到這兩個平面的距離相等,則這兩個圓的半徑之和為( )
.若球心到這兩個平面的距離相等,則這兩個圓的半徑之和為( )
A. 4B. 6C. 8D. 10
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有甲、乙、丙三名學生參加某大學的自主招生考試,考試分兩輪,第一輪筆試,第二輪面試,只有第一輪筆試通過才有資格進入第二輪面試,面試通過就可以在高考錄取中獲得該校的優惠加分,兩輪考試相互獨立.根據以往多次的模擬測試,甲、乙、丙三名學生能通過筆試的概率分別為0.4,0.8,0.5,能通過面試的概率分別為0.8,0.4,0.64.根據這些數據我們可以預測:
(1)甲、乙、丙三名學生中至少有兩名學生通過第一輪筆試的概率;
(2)甲、乙、丙三名學生能獲得該校優惠加分的人數![]() 的數學期望.
的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com