
【題目】已知函數![]() 是偶函數
是偶函數
(1)求k的值;
(2)若函數![]() 的圖象與直線
的圖象與直線![]() 沒有交點,求b的取值范圍;
沒有交點,求b的取值范圍;
(3)設![]() ,若函數
,若函數![]() 與
與![]() 的圖象有且只有一個公共點,求實數
的圖象有且只有一個公共點,求實數![]() 的取值范圍
的取值范圍
【答案】(1)![]() (2)
(2)![]() (3)
(3)![]()
【解析】
試題(1)因為函數![]() 是偶函數,所以根據偶函數的定義,得到一個關于x,k的等式.由于對于任意的x都成立,相當于恒過定點的問題,所以求得k的值.
是偶函數,所以根據偶函數的定義,得到一個關于x,k的等式.由于對于任意的x都成立,相當于恒過定點的問題,所以求得k的值.
(2)因為函數![]() 的圖象與直線
的圖象與直線![]() 沒有交點,所以對應的方程沒有解,利用分離變量的思維可得到一個等式
沒有交點,所以對應的方程沒有解,利用分離變量的思維可得到一個等式![]() ,該方程無解.所以等價兩個函數
,該方程無解.所以等價兩個函數![]() 與
與![]() 沒有交點,所以求出函數
沒有交點,所以求出函數![]() 的最值.即可得到b的取值范圍.
的最值.即可得到b的取值范圍.
(3)因為![]() ,若函數
,若函數![]() 與
與![]() 的圖象有且只有一個公共點,所以等價于方程
的圖象有且只有一個公共點,所以等價于方程![]() 有且只有一個實數根.通過換元
有且只有一個實數根.通過換元![]() 將原方程化為含參的二次方程的形式,即等價于該二次方程僅有一個大于零的實根,通過討論即可得到結論.
將原方程化為含參的二次方程的形式,即等價于該二次方程僅有一個大于零的實根,通過討論即可得到結論.
試題解析:(1)因為![]() 為偶函數,所以
為偶函數,所以![]() ,
,
即![]() 對于任意
對于任意![]() 恒成立.
恒成立.
于是![]() 恒成立,
恒成立,
而![]() 不恒為零,所以
不恒為零,所以![]() .
.
(2)由題意知方程![]() 即方程
即方程![]() 無解.
無解.
令![]() ,則函數
,則函數![]() 的圖象與直線
的圖象與直線![]() 無交點.
無交點.
因為![]() ,由
,由![]() ,則
,則![]() ,
,
所以![]() 的取值范圍是
的取值范圍是![]() .
.
(3)由題意知方程![]() 有且只有一個實數根.
有且只有一個實數根.
令![]() ,則關于
,則關于![]() 的方程
的方程![]() (記為(*))有且只有一個正根.
(記為(*))有且只有一個正根.
若![]() ,則
,則![]() ,不合題意, 舍去;
,不合題意, 舍去;
若![]() ,則方程(*)的兩根異號或有兩相等正根.
,則方程(*)的兩根異號或有兩相等正根.
由![]() 或
或![]() ;但
;但![]() ,不合題意,舍去;而
,不合題意,舍去;而![]() ;
;
若方程(*)的兩根異號![]()
綜上所述,實數![]() 的取值范圍是
的取值范圍是![]() .
.


 探究與鞏固河南科學技術出版社系列答案
探究與鞏固河南科學技術出版社系列答案科目:高中數學 來源: 題型:
【題目】將函數y=2cos(2x+![]() )的圖象向左平移
)的圖象向左平移![]() 個單位長度,得到函數y=f(x)的圖象.
個單位長度,得到函數y=f(x)的圖象.
(1)求f(x)的單調遞增區(qū)間;
(2)求f(x)在[0,![]() ]上的值域.
]上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x3-2x2+3x(x∈R)的圖象為曲線C.
x3-2x2+3x(x∈R)的圖象為曲線C.
(1)求過曲線C上任意一點切線斜率的取值范圍;
(2)若在曲線C上存在兩條相互垂直的切線,求其中一條切線與曲線C的切點的橫坐標的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了改善市民的生活環(huán)境,長沙某大型工業(yè)城市決定對長沙市的1萬家中小型化工企業(yè)進行污染情況摸排,并出臺相應的整治措施.通過對這些企業(yè)的排污口水質,周邊空氣質量等的檢驗,把污染情況綜合折算成標準分100分,發(fā)現長沙市的這些化工企業(yè)污染情況標準分基本服從正態(tài)分布N(50,162),分值越低,說明污染越嚴重;如果分值在[50,60]內,可以認為該企業(yè)治污水平基本達標.
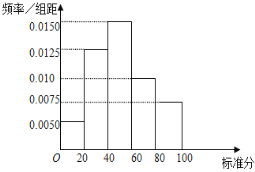
(Ⅰ)如圖為長沙市的某工業(yè)區(qū)所有被調査的化工企業(yè)的污染情況標準分的頻率分布直方圖,請計算這個工業(yè)區(qū)被調査的化工企業(yè)的污染情況標準分的平均值,并判斷該工業(yè)區(qū)的化工企業(yè)的治污平均值水平是否基本達標;
(Ⅱ)大量調査表明,如果污染企業(yè)繼續(xù)生產,那么標準分低于18分的化工企業(yè)每月對周邊造成的直接損失約為10萬元,標準分在[18,34)內的化工企業(yè)每月對周邊造成的直接損失約為4萬元.長沙市決定關停80%的標準分低于18分的化工企業(yè)和60%的標準分在[18,34)內的化工企業(yè),每月可減少的直接損失約有多少?
(附:若隨機變量![]() ,則
,則![]() ,
, ![]() ,
,![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】通過市場調查,得到某種產品的資金投入![]() (單位:萬元)與獲得的利潤
(單位:萬元)與獲得的利潤![]() (單位:千元)的數據,如表所示
(單位:千元)的數據,如表所示
資金投入 | 2 | 3 | 4 | 5 |
利潤 | 2 | 3 | 5 | 6 |
(1)根據上表提供的數據,用最小二乘法求線性回歸直線方程![]() ;
;
(2)該產品的資金投入每增加![]() 萬元,獲得利潤預計可增加多少千元?若投入資金
萬元,獲得利潤預計可增加多少千元?若投入資金![]() 萬元,則獲得利潤的估計值為多少千元?
萬元,則獲得利潤的估計值為多少千元?
參考公式:
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設a為實數,函數f(x)=ex﹣2x+2a,x∈R.
(1)求f(x)的單調區(qū)間及極值;
(2)求證:當a>ln2﹣1且x>0時,ex>x2﹣2ax+1.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,已知直線
中,已知直線![]() :
: (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() 的直角坐標為
的直角坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 的交點為
的交點為![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】等比數列{an}的各項均為正數,且2a1+3a2=1, ![]() =9a2a6.
=9a2a6.
(1)求數列{an}的通項公式;
(2)設bn=log3a1+log3a2+…+log3an,求數列![]() 的前n項和.
的前n項和.
查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com