
【題目】一個盒子中裝有四張卡片,每張卡片上寫有一個數字,數字分別是![]() ,現從盒子中隨機抽取卡片,每張卡片被抽到的概率相等.
,現從盒子中隨機抽取卡片,每張卡片被抽到的概率相等.
(1)若一次抽取三張卡片,求抽到的三張卡片上的數字之和大于![]() 的概率;
的概率;
(2)若第一次抽一張卡片,放回后攪勻再抽取一張卡片,求兩次抽取中至少有一次抽到寫有數字![]() 的卡片的概率.
的卡片的概率.
 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】設點![]() 為橢圓
為橢圓![]() 的左焦點,直線
的左焦點,直線![]() 被橢圓
被橢圓![]() 截得弦長為
截得弦長為![]() .
.
(1)求橢圓![]() 的方程;
的方程;
(2)圓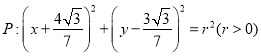 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點, ![]() 為線段
為線段![]() 上任意一點,直線
上任意一點,直線![]() 交橢圓
交橢圓![]() 于
于![]() 兩點
兩點![]() 為圓
為圓![]() 的直徑,且直線
的直徑,且直線![]() 的斜率大于
的斜率大于![]() ,求
,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若函數f(x)滿足f(logax)=![]() ·(x-
·(x-![]() )(其中a>0且a≠1).
)(其中a>0且a≠1).
(1)求函數f(x)的解析式,并判斷其奇偶性和單調性;
(2)當x∈(-∞,2)時,f(x)-4的值恒為負數,求a的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某種產品的廣告費支出![]() 與銷售額
與銷售額![]() (單位:萬元)具有較強的相關性,且兩者之間有如下對應數據:
(單位:萬元)具有較強的相關性,且兩者之間有如下對應數據:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
(1)求![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)根據(1)中的線性回歸方程,當廣告費支出為10萬元時,預測銷售額是多少?
參考數據: ![]() ,
,![]() ,
,![]() 。
。
附:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
 ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為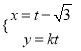 (
(![]() 為參數),直線
為參數),直線![]() 的參數程為
的參數程為 (
(![]() 為參數),設直線
為參數),設直線![]() 與
與![]() 的交點為
的交點為![]() ,當
,當![]() 變化時點
變化時點![]() 的軌跡為曲線
的軌跡為曲線![]() .
.
(1)求出曲線![]() 的普通方程;
的普通方程;
(2)以坐標原點為極點, ![]() 軸的正半軸為極軸建立極坐標系,直線
軸的正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() ,點
,點![]() 為曲線
為曲線![]() 的動點,求點
的動點,求點![]() 到直線
到直線![]() 的距離的最小值.
的距離的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com