
【題目】某花店每天以每枝5元的價格從農場購進若干枝玫瑰花,然后以每枝10元的價格出售,如果當天賣不完,剩下的玫瑰花作垃圾處理.
(Ⅰ)若花店一天購進17枝玫瑰花,求當天的利潤![]() (單位:元)關于當天需求量
(單位:元)關于當天需求量![]() (單位:枝,
(單位:枝, ![]() )的函數解析式.
)的函數解析式.
(Ⅱ)花店記錄了100天玫瑰花的日需求量(單位:枝),整理得下表:
![]()
以100天記錄的各需求量的頻率作為各需求量發生的概率.
(1)若花店一天購進17枝玫瑰花, ![]() 表示當天的利潤(單位:元),求
表示當天的利潤(單位:元),求![]() 的分布列及數學期望;
的分布列及數學期望;
(2)若花店計劃一天購進16枝或17枝玫瑰花,以利潤角度看,你認為應購進16枝好還是17枝好?請說明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)(1)答案見解析;(2)應購進17枝,理由見解析.
;(Ⅱ)(1)答案見解析;(2)應購進17枝,理由見解析.
【解析】試題分析:
(Ⅰ)根據題意將問題用分段函數的形式表示出來即可.(Ⅱ)(1) 由題意得![]() 的所有可能取值,并求出每個取值的概率,列成表格的形式可得分布列,然后可求得期望;(2)由題意得當購進16枝玫瑰花時,當天的利潤為
的所有可能取值,并求出每個取值的概率,列成表格的形式可得分布列,然后可求得期望;(2)由題意得當購進16枝玫瑰花時,當天的利潤為![]() ,然后與(1)作比較后可得結論.
,然后與(1)作比較后可得結論.
試題解析:
(Ⅰ)當日需求量![]() 時,可得利潤
時,可得利潤![]() ;
;
當日需求量![]() 時,可得利潤
時,可得利潤![]() ,
,
綜上可得![]() 關于
關于![]() 的解析式為
的解析式為![]() ;
;
(Ⅱ)(1)由題意得![]() 的所有可能取值為55,65,75,85,
的所有可能取值為55,65,75,85,
![]() ,
, ![]() ,
,
![]() ,
, ![]()
∴隨機變量![]() 的分布列為:
的分布列為:

∴![]() .
.
(2)由題意得當購進16枝玫瑰花時,當天的利潤為
![]()
![]() ,
,
∵![]() ,
,
∴應購進17枝玫瑰花.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】如圖所示為一正方體的平面展開圖,在這個正方體中,有下列四個命題:
①AF⊥GC;
②BD與GC成異面直線且夾角為60;
③BD∥MN;
④BG與平面ABCD所成的角為45.
其中正確的個數是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司計劃購買2臺機器,該種機器使用三年后即被淘汰.機器有一易損零件,在購進機器時,可以額外購買這種零件作為備件,每個200元.在機器使用期間,如果備件不足再購買,則每個500元.現需決策在購買機器時應同時購買幾個易損零件,為此搜集并整理了100臺這種機器在三年使用期內更換的易損零件數,得下面柱狀圖:

以這100臺機器更換的易損零件數的頻率代替1臺機器更換的易損零件數發生的概率,記X表示2臺機器三年內共需更換的易損零件數,n表示購買2臺機器的同時購買的易損零件數.
(1)求X的分布列;
(2)若要求P(X≤n)≤0.5,確定n的最小值;
(3)以購買易損零件所需費用的期望值為決策依據,在n=19與n=20之中選其一,應選用哪個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設S是實數集R的非空子集,若對任意x,y∈S,都有x+y,x-y,xy∈S,則稱S為封閉集.下列命題:①集合S={a+b![]() |a,b為整數}為封閉集;②若S為封閉集,則一定有0∈S;③封閉集一定是無限集;④若S為封閉集,則滿足STR的任意集合T也是封閉集.其中真命題是________.(寫出所有真命題的序號)
|a,b為整數}為封閉集;②若S為封閉集,則一定有0∈S;③封閉集一定是無限集;④若S為封閉集,則滿足STR的任意集合T也是封閉集.其中真命題是________.(寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在“新零售”模式的背景下,某大型零售公司為推廣線下分店,計劃在![]() 市的
市的![]() 區開設分店.為了確定在該區開設分店的個數,該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格.記
區開設分店.為了確定在該區開設分店的個數,該公司對該市已開設分店的其他區的數據作了初步處理后得到下列表格.記![]() 表示在各區開設分店的個數,
表示在各區開設分店的個數, ![]() 表示這
表示這![]() 個分店的年收入之和.
個分店的年收入之和.
| 2 | 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 | 6 |
(Ⅰ)該公司已經過初步判斷,可用線性回歸模型擬合![]() 與
與![]() 的關系,求
的關系,求![]() 關于
關于![]() 的線性回歸方程;
的線性回歸方程;
(Ⅱ)假設該公司在![]() 區獲得的總年利潤
區獲得的總年利潤![]() (單位:百萬元)與
(單位:百萬元)與![]() 之間的關系為
之間的關系為![]() ,請結合(Ⅰ)中的線性回歸方程,估算該公司應在
,請結合(Ⅰ)中的線性回歸方程,估算該公司應在![]() 區開設多少個分店,才能使
區開設多少個分店,才能使![]() 區平均每個分店的年利潤最大?
區平均每個分店的年利潤最大?
參考公式:
![]() ,
, 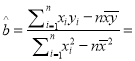
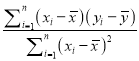 ,
, ![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來我國電子商務行業迎來發展的新機遇,2017年雙11全天交易額達到1682億元,為規范和評估該行業的情況,相關管理部門制定出針對電商的商品和服務的評價體系.現從評價系統中選出200次成功交易,并對其評價進行評價,對商品的好評率為0.6,對服務的好評率為0.75,其中對商品和服務都做出好評的交易為80次.
(1)完成關于商品和服務評價的![]() 列聯表,判斷能否在犯錯誤的概率不超過0.001的前提下,認為商品好評與服務好評有關?
列聯表,判斷能否在犯錯誤的概率不超過0.001的前提下,認為商品好評與服務好評有關?
(2)若將頻率視為概率,某人在該購物平臺上進行的3次購物中,設對商品和服務全為好評的次數為隨機變量![]() :
:
①求對商品和服務全為好評的次數![]() 的分布列;
的分布列;
②求![]() 的數學期望和方差.
的數學期望和方差.
附:臨界值表:

![]() 的觀測值:
的觀測值: 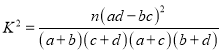 (其中
(其中![]() )
)
關于商品和服務評價的![]() 列聯表:
列聯表:

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com