
【題目】已知函數![]()
![]() .
.
(Ⅰ) 求函數![]() 的單調區間;
的單調區間;
(Ⅱ) 當![]() 時,求函數
時,求函數![]() 在
在![]() 上最小值.
上最小值.
【答案】(Ⅰ)見解析;(Ⅱ)當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() ;當
;當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]()
【解析】
(1)求出導函數,并且解出它的零點x=,再分區間討論導數的正負,即可得到函數f(x)的單調區間;
(2)分三種情況加以討論,結合函數的單調性與函數值的大小比較,即可得到當0<a<ln 2時,函數f(x)的最小值是-a;當a≥ln2時,函數f(x)的最小值是ln2-2a.
![]() 函數
函數![]() 的定義域為
的定義域為![]() .
.![]()
因為![]() ,令
,令![]() ,可得
,可得![]() ;
;
當![]() 時,
時,![]() ;當
;當![]() 時,
時,![]() ,
,
綜上所述:可知函數![]() 的單調遞增區間為
的單調遞增區間為![]() ,單調遞減區間為
,單調遞減區間為![]()
![]() 當
當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上是減函數,
上是減函數,![]() 的最小值是
的最小值是![]()
![]() 當
當![]() ,即
,即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上是增函數,
上是增函數,
![]() 的最小值是
的最小值是![]()
![]() 當
當![]() ,即
,即![]() 時,函數
時,函數![]() 在
在![]() 上是增函數,在
上是增函數,在![]() 上是減函數.
上是減函數.
又![]() ,
,![]() 當
當![]() 時,
時,![]() 的最小值是
的最小值是![]() ;
;
當![]() 時,
時,![]() 的最小值為
的最小值為![]()
綜上所述,結論為當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() ;
;
當![]() 時,函數
時,函數![]() 的最小值是
的最小值是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】幾位大學生響應國家的創業號召,開發了一款應用軟件.為激發大家學習數學的興趣,他們推出了“解數學題獲取軟件激活碼”的活動.這款軟件的激活碼為下面數學問題的答案:已知數列1,1,2,1,2,4,1,2,4,8,1,2,4,8,16,…,其中第一項是20,接下來的兩項是20,21,再接下來的三項是20,21,22,依此類推.求滿足如下條件的最小整數N:N>100且該數列的前N項和為2的整數冪.那么該款軟件的激活碼是
A. 440B. 330
C. 220D. 110
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】十三屆全國人大二次會議于2019年3月5日在京召開.為了了解某校大學生對兩會的關注程度,學校媒體在開幕后的第二天,從學生中隨機抽取了180人,對是否收看2019年兩會開幕會情況進行了問卷調查,統計數據得到列聯表如下:
收看 | 沒收看 | 合計 | |
男生 | 40 | ||
女生 | 30 | 60 | |
合計 |
(1)請完成列聯表;
(2)根據上表說明,能否有99%的把握認為該校大學生收看開幕會與性別有關?(結果精確到0.001)
附: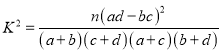 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.01 | 0.005 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱柱ABC﹣A'B'C',AC=2,BC=4,∠ACB=120°,∠ACC'=90°,且平面AB'C⊥平面ABC,二面角A'﹣AC﹣B'為30°,E、F分別為A'C、B'C'的中點.

(1)求證:EF∥平面AB'C;
(2)求B'到平面ABC的距離;
(3)求二面角A﹣BB'﹣C'的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某公司近年來科研費用支出![]() 萬元與公司所獲得利潤
萬元與公司所獲得利潤![]() 萬元之間有如下的統計數據:
萬元之間有如下的統計數據:
x | 2 | 3 | 4 | 5 |
Y | 18 | 27 | 32 | 35 |
(1)請根據上表提供的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(2)試根據(1)求出的線性回歸方程,預測該公司科研費用支出為10萬元時公司所獲得的利潤.
參考公式:用最小二乘法求線性回歸方程![]() 的系數公式:
的系數公式:
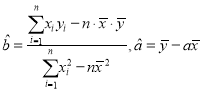
參考數據:2×18+3×27+4×32+5×35=420
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】△ABC的內角A,B,C的對邊分別為a,b,c,已知△ABC的面積為![]()
(1)求sinBsinC;
(2)若6cosBcosC=1,a=3,求△ABC的周長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(Ⅰ)若函數f(x)的最小值為8,求實數a的值;
(Ⅱ)若函數g(x)=|f(x)|+f(x)﹣16有4個零點,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com