
 )=f(-t+
)=f(-t+ ).記g(x)=Acos(ωx+φ)-1,則g(
).記g(x)=Acos(ωx+φ)-1,則g( )= .
)= . 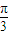 )=f(-t+
)=f(-t+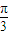 ).我們易得:函數f(x)的圖象關于直線x=
).我們易得:函數f(x)的圖象關于直線x=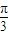 對稱,則ω
對稱,則ω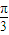 +φ的終邊落在Y軸上,將其代入g(x)=Acos(ωx+φ)-1,我們易得g(
+φ的終邊落在Y軸上,將其代入g(x)=Acos(ωx+φ)-1,我們易得g(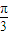 )的值.
)的值. )=f(-t+
)=f(-t+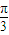 ).
).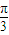 對稱
對稱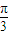 +φ=kπ+
+φ=kπ+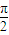 ,k∈Z
,k∈Z )=Acos(ω
)=Acos(ω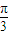 +φ)-1
+φ)-1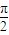 )-1=-1
)-1=-1

 導學教程高中新課標系列答案
導學教程高中新課標系列答案 小學課時特訓系列答案
小學課時特訓系列答案科目:高中數學 來源: 題型:
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
| π |
| 3 |
| π |
| 3 |
| π |
| 3 |
查看答案和解析>>
科目:高中數學 來源:2009-2010學年數學寒假作業(04)(解析版) 題型:填空題
 )=f(-t+
)=f(-t+ ).記g(x)=Acos(ωx+φ)-1,則g(
).記g(x)=Acos(ωx+φ)-1,則g( )= .
)= .查看答案和解析>>
科目:高中數學 來源:2012年廣東省江門市恩平市附城中學高考二輪復習綜合試卷(文科)(解析版) 題型:解答題
 )=f(-t+
)=f(-t+ ).記g(x)=Acos(ωx+φ)-1,則g(
).記g(x)=Acos(ωx+φ)-1,則g( )= .
)= .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com