
【題目】若函數![]() 存在極值,且這些極值的和不小于
存在極值,且這些極值的和不小于![]() ,則
,則![]() 的取值范圍為( )
的取值范圍為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】f(x)=ax﹣x2﹣lnx,x∈(0,+∞),
則f′(x)=a﹣2x﹣![]() ,
,
∵函數f(x)存在極值,∴f′(x)=0在(0,+∞)上有根,
即2x2﹣ax+1=0在(0,+∞)上有根,∴△=a2﹣8≥0,
顯然當△=0時,F(x)無極值,不合題意;
∴方程必有兩個不等正根,記方程2x2﹣ax+1=0的兩根為x1,x2,x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
f(x1),f(x2)是函數F(x)的兩個極值,
由題意得,f(x1)+f(x2)=a(x1+x2)﹣(x12+x22)﹣(lnx1+lnx2)
=![]() ﹣
﹣![]() +1﹣ln
+1﹣ln![]()
![]() 4﹣ln
4﹣ln![]() ,
,
化簡解得,a2![]() 12,滿足△>0,
12,滿足△>0,
又x1+x2=![]() >0,即a>0,
>0,即a>0,
∴a的取值范圍是[![]() ,+∞),
,+∞),
故答案為:C。


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐P-ABCD中,AB//CD,且![]()

(1)證明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,且四棱錐P-ABCD的體積為
,且四棱錐P-ABCD的體積為![]() ,求該四棱錐的側面積.
,求該四棱錐的側面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現從某學校高一年級男生中隨機抽取50名測量身高,測量發現被測學生身高全部介于![]() 和
和![]() 之間,將測量結果按如下方式分成6組:第1組
之間,將測量結果按如下方式分成6組:第1組![]() ,第2組
,第2組![]() ,…,第6組
,…,第6組![]() ,下圖是按上述分組方法得到的頻率分布直方圖.
,下圖是按上述分組方法得到的頻率分布直方圖.
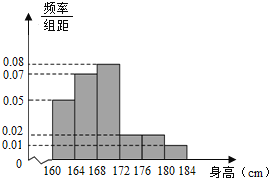
(1)求這50名男生身高的中位數,并估計該校高一全體男生的平均身高;
(2)求這50名男生當中身高不低于176![]() 的人數,并且在這50名身高不低于176
的人數,并且在這50名身高不低于176![]() 的男生中任意抽取2人,求這2人身高都低于180
的男生中任意抽取2人,求這2人身高都低于180![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的一個焦點在直線
的一個焦點在直線![]() 上,且離心率
上,且離心率![]() .
.
(1)求該橢圓的方程;
(2)若![]() 與
與![]() 是該橢圓上不同的兩點,且線段
是該橢圓上不同的兩點,且線段![]() 的中點
的中點![]() 在直線
在直線![]() 上,試證:
上,試證: ![]() 軸上存在定點
軸上存在定點![]() ,對于所有滿足條件的
,對于所有滿足條件的![]() 與
與![]() ,恒有
,恒有![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】有下列命題:(1)終邊相同的角的同名三角比的值相等;(2)終邊不同的角的同名三角比的值不同;(3)若![]() ,則
,則![]() 是第一或第二象限角;(4)△
是第一或第二象限角;(4)△![]() 中,若
中,若![]() ,則
,則![]() ;其中正確命題的個數是( )
;其中正確命題的個數是( )
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在高中學習過程中,同學們常這樣說:“如果你的物理成績好,那么你的數學學習就不會有什么大問題.”某班針對“高中物理學習對數學學習的影響”進行研究,得到了學生的物理成績與數學成績具有線性相關關系,如表為該班隨機抽取6名學生在一次考試中的物理和數學成績:
學生編號 學科 | 1 | 2 | 3 | 4 | 5 | 6 |
物理成績(x) | 75 | 65 | 75 | 65 | 60 | 80 |
數學成績(y) | 125 | 117 | 110 | 103 | 95 | 110 |
(1)求數學成績y對物理成績x的線性回歸方程;
(2)該班某同學的物理成績100分,預測他的數學成績.
參考公式:回歸方程![]() 中斜率和截距的最小二乘估計公式分別為:
中斜率和截距的最小二乘估計公式分別為:
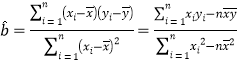 ,
,![]()
參考數據:752+652+752+652+602+802=29700,
75×125+65×117+75×110+65×103+60×95+80×110=46425.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com