
【題目】將函數![]() 的圖象向右平移
的圖象向右平移![]() (
(![]() )個單位長度后得到函數
)個單位長度后得到函數![]() 的圖象,若
的圖象,若![]() 在區間
在區間![]() 上單調遞增,則實數
上單調遞增,則實數![]() 的取值范圍是( )
的取值范圍是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】D
【解析】分析:根據平移關系求出g(x)的解析式,結合函數的單調性建立不等式關系進行求解即可.
詳解:將函數f(x)=sin2x的圖象向右平移φ(0<![]() <
<![]() )個單位長度后得到函數g(x)的圖象,
)個單位長度后得到函數g(x)的圖象,
則g(x)=sin2(x﹣![]() )=sin(2x﹣2
)=sin(2x﹣2![]() ),
),
若g(x)在區間[0,![]() ]上單調遞增,
]上單調遞增,
則2kπ﹣![]() ≤2x﹣2
≤2x﹣2![]() ≤2kπ+
≤2kπ+![]() ,k∈Z,
,k∈Z,
得2kπ﹣![]() +2
+2![]() ≤2x≤2kπ+
≤2x≤2kπ+![]() +2
+2![]() ,k∈Z,
,k∈Z,
即kπ﹣![]() +
+![]() ≤x≤kπ+
≤x≤kπ+![]() +
+![]() ,k∈Z,
,k∈Z,
即函數的單調遞增區間為[kπ﹣![]() +
+![]() ,kπ+
,kπ+![]() +
+![]() ],k∈Z,
],k∈Z,
∵若g(x)在區間[0,![]() ]上單調遞增,
]上單調遞增,
∴滿足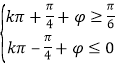 ,即
,即 ,
,
則﹣kπ﹣![]() ≤
≤![]() ≤﹣kπ+
≤﹣kπ+![]() ,k∈Z,
,k∈Z,
當k=0時,﹣![]() ≤
≤![]() ≤
≤![]() ,
,
又因為:0<![]() <
<![]()
所以![]() 的取值范圍是(0,
的取值范圍是(0,![]() ],
],
故選:D.


科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() 為實常數).
為實常數).

(1)當![]() 時,作出
時,作出![]() 的圖象,并寫出它的單調遞增區間;
的圖象,并寫出它的單調遞增區間;
(2)設![]() 在區間
在區間![]() 的最小值為
的最小值為![]() ,求
,求![]() 的表達式;
的表達式;
(3)已知函數![]() 在
在![]() 的情況下:其在區間
的情況下:其在區間![]() 單調遞減,在區間
單調遞減,在區間![]() 單調遞增.設
單調遞增.設![]() ,若函數
,若函數![]() 在區間
在區間![]() 上是增函數,求實數
上是增函數,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一條街道上有10盞路燈,將路燈依次排列并編號1到10.有關部門要求晚上這10盞路燈中相鄰的兩盞燈不能全開,且這10盞路燈中至少打開兩盞路燈.則符合要求的開法總數______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列說法:①對于獨立性檢驗,![]() 的值越大,說明兩事件相關程度越大;②以模型
的值越大,說明兩事件相關程度越大;②以模型![]() 去擬合一組數據時,為了求出回歸方程,設
去擬合一組數據時,為了求出回歸方程,設![]() ,將其變換后得到線性方程
,將其變換后得到線性方程![]() ,則
,則![]() ,
,![]() 的值分別是
的值分別是![]() 和
和![]() ;③根據具有線性相關關系的兩個變量的統計數據所得的回歸直線方程
;③根據具有線性相關關系的兩個變量的統計數據所得的回歸直線方程![]() 中,
中,![]() ,
,![]() ,
,![]() ,則
,則![]() ;④通過回歸直線
;④通過回歸直線![]() 及回歸系數
及回歸系數![]() ,可以精確反映變量的取值和變化趨勢,其中正確的個數是( )
,可以精確反映變量的取值和變化趨勢,其中正確的個數是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在三棱柱![]() 中,底面ABC為正三角形,
中,底面ABC為正三角形,![]() 底面ABC,
底面ABC,![]() ,點
,點![]() 在線段
在線段![]() 上,平面
上,平面![]() 平面
平面![]() .
.

(1)請指出點![]() 的位置,并給出證明;
的位置,并給出證明;
(2)若![]() ,求
,求![]() 與平面ABE夾角的正弦值.
與平面ABE夾角的正弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com