【題目】已知函數
（
），
．
（1）求函數
單調區間；
（2）當
時，
①求函數在
上的值域；
②求證：
，其中
，
．（參考數據
）
【答案】(1)見解析;(2) ①
；②見解析.
【解析】試題分析: （1）先求導數，再研究導函數符號：當
時，恒為正；當
時，有正有負，根據符號規律確定單調區間，（2）①易得函數
在
單調性：先減后增，故在極小值點處取最小值，最大值為兩端點值的較大值，②由所證不等式的結構知，先研究數列求和：令
，可得
，再比較對應項大小：
,這樣轉化為證明不等式
,利用導數研究函數
單調性，即可證得.
試題解析:（1）∵
．
①當時，
，在
單調遞增；
②當時，令
，得
，即
，
∴在
上單調遞減，在
單調遞增．
（2）
時，
．
①由
，令
，
∴在
單調遞減，
單調遞增，且由
，
，
∴值域為
．
②由
，設為
前
項和，
，
則
，
設，
，
在
單調遞減，
，∴
，
∴
，即時，
，
∴
，故原不等式成立．
科學實驗活動冊系列答案科目：高中數學 來源： 題型：
【題目】《中華人民共和國個人所得稅法》規定，公民全月工資所得不超過3500元的部分不必納稅，超過3500元的部分為全月應納稅所得額。此項稅款按下表分段累計計算：
全月應納稅所得額 | 稅率（％） |
不超過1500元的部分 | 3 |
超過1500元至4500元的部分 | 10 |
超過4500元至9000元的部分 | 20 |
(1)某人10月份應交此項稅款為350元，則他10月份的工資收入是多少？
(2)假設某人的月收入為
元， 
，記他應納稅為
元，求
的函數解析式.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數列
的前
項和為
，且滿足
，求數列
的通項公式．勤于思考的小紅設計了下面兩種解題思路，請你選擇其中一種并將其補充完整．
思路1：先設
的值為1，根據已知條件，計算出
_________， 
__________， 
_________．
猜想： 
_______.
然后用數學歸納法證明．證明過程如下：
①當
時，________________，猜想成立
②假設
（
N*）時，猜想成立，即
_______．
那么，當
時，由已知
，得
_________．
又
，兩式相減并化簡，得
_____________（用含
的代數式表示）．
所以，當
時，猜想也成立．
根據①和②，可知猜想對任何
N*都成立．
思路2：先設
的值為1，根據已知條件，計算出
_____________．
由已知
，寫出
與
的關系式： 
_____________________，
兩式相減，得
與
的遞推關系式： 
____________________．
整理： 
____________．
發現：數列
是首項為________，公比為_______的等比數列．
得出：數列
的通項公式
____，進而得到
____________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f(x)＝
.
(1)求f(2)與f
， f(3)與f
；
(2)由(1)中求得結果，你能發現f(x)與f
有什么關系？并證明你的發現；
(3)求f(1)＋f(2)＋f(3)＋…＋f(2013)＋f
＋f
＋…＋f
.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】甲、乙、丙、丁四個物體同時從某一點出發向同一個方向運動，其路程
關于時間
的函數關系式分別為
， 
， 
， 
，有以下結論：
①當
時，甲走在最前面；
②當
時，乙走在最前面；
③當
時,丁走在最前面，當
時，丁走在最后面；
④丙不可能走在最前面，也不可能走在最后面；
⑤如果它們一直運動下去，最終走在最前面的是甲．
其中，正確結論的序號為 （把正確結論的序號都填上,多填或少填均不得分）．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】選修4-4：坐標系與參數方程
在平面直角坐標系
中，曲線
： 
，曲線
： 
（
為參數），以坐標原點
為極點， 
軸正半軸為極軸，建立極坐標系.
（Ⅰ）求曲線
， 
的極坐標方程；
（Ⅱ）曲線
： 
（
為參數， 
， 
）分別交
， 
于
， 
兩點，當
取何值時， 
取得最大值.
查看答案和解析>>
科目：高中數學 來源： 題型：
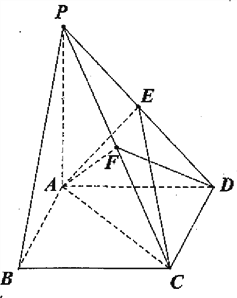
【題目】如圖，四棱錐P—ABCD的底面ABCD為矩形，PA⊥平面ABCD，點E是棱PD的中點，點F是PC的中點．
（Ⅰ）證明：PB∥平面AEC；
（Ⅱ）若底面ABCD為正方形，
，求二面角C—AF—D大小．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
