
【題目】在等比數列![]() 中,已知
中,已知![]() 設數列
設數列![]() 的前n項和為
的前n項和為![]() ,且
,且![]()
(1)求數列![]() 通項公式;
通項公式;
(2)證明:數列![]() 是等差數列;
是等差數列;
(3)是否存在等差數列![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ?若存在,求出所有符合題意的等差數列
?若存在,求出所有符合題意的等差數列![]() ;若不存在,請說明理由.
;若不存在,請說明理由.
【答案】(1)![]() ;(2)詳見解析;(3)存在,且
;(2)詳見解析;(3)存在,且![]() .
.
【解析】
(1)根據已知條件求得![]() ,由此求得數列
,由此求得數列![]() 通項公式.
通項公式.
(2)利用 ,證得數列
,證得數列![]() 是等差數列.
是等差數列.
(3)由(2)求得![]() 和
和![]() ,假設存在符合題意的等差數列
,假設存在符合題意的等差數列![]() ,結合
,結合![]() 求得
求得![]() .
.
(1)依題意 ,解得
,解得![]() ,所以
,所以![]() .
.
(2)依題意![]() ,
,![]() ,即
,即![]() ①,
①,
所以![]() ②,
②,
②-①并化簡得![]() ,
,
故 ,即
,即![]() .
.
令![]() 代入
代入![]() 得
得
![]() .
.
所以![]() .所以
.所以![]() .
.
所以數列![]() 是以
是以![]() 為首項,公差為
為首項,公差為![]() 的等差數列.
的等差數列.
(3)由(2)得![]() ,所以
,所以![]() .
.
所以![]() .
.
假設存在滿足題意的等差數列![]() ,使得對任意
,使得對任意![]() ,都有
,都有![]() ,設
,設![]() ,
,
即對任意![]() ,都有
,都有![]() ,即
,即![]() ③.
③.
首先證明滿足③的![]() :
:
(i)當![]() 時,若
時,若![]() ,
,![]() ,則
,則![]() ,不滿足③;
,不滿足③;
(ii)當![]() 時,若
時,若![]() ,
,![]() ,則
,則![]() .
.
而![]() ,則
,則![]() ,
,
所以![]() ,則
,則![]() ,不滿足③;
,不滿足③;
所以![]() .
.
令![]() ,
,![]() ,
,
所以![]() 在
在![]() 上遞增.
上遞增.
所以當![]() 時,
時,![]() .
.
即當![]() 時,
時,![]() ,即
,即![]() .
.
所以當![]() ,
,![]() 時,
時,![]() .
.
再證明![]() :
:
(iii)若![]() ,則當
,則當![]() 時,
時,![]() ,
,![]() ,這與③矛盾.
,這與③矛盾.
(iv)若![]() ,同(i)可得矛盾.所以
,同(i)可得矛盾.所以![]() .
.
當![]() 時,
時,![]() ,滿足
,滿足![]() ,所以
,所以![]() .
.
綜上所述,存在唯一的等差數列![]() ,其通項公式為
,其通項公式為![]() ,滿足題設.
,滿足題設.


 新課標快樂提優暑假作業陜西旅游出版社系列答案
新課標快樂提優暑假作業陜西旅游出版社系列答案 暑假銜接培優教材浙江工商大學出版社系列答案
暑假銜接培優教材浙江工商大學出版社系列答案 欣語文化快樂暑假沈陽出版社系列答案
欣語文化快樂暑假沈陽出版社系列答案科目:高中數學 來源: 題型:
【題目】2019年底,湖北省武漢市等多個地區陸續出現感染新型冠狀病毒肺炎的患者.為及時有效地對疫情數據進行流行病學統計分析,某地研究機構針對該地實際情況,根據該地患者是否有武漢旅行史與是否有確診病例接觸史,將新冠肺炎患者分為四類:有武漢旅行史(無接觸史),無武漢旅行史(無接觸史),有武漢旅行史(有接觸史)和無武漢旅行史(有接觸史),統計得到以下相關數據.
(1)請將列聯表填寫完整:
有接觸史 | 無接觸史 | 總計 | |
有武漢旅行史 | 27 | ||
無武漢旅行史 | 18 | ||
總計 | 27 | 54 |
(2)能否在犯錯誤的概率不超過0.025的前提下認為有武漢旅行史與有確診病例接觸史有關系?
附:![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“中國剩余定理”又稱“孫子定理”,最早可見于中國南北朝時期的數學著作《孫子算經》卷下第二十六題,叫做“物不知數”,原文如下:今有物不知其數,三三數之剩二,五五數之剩三,七七數之剩二,問物幾何?現有這樣一個相關的問題:將1到2020這2020個自然數中滿足被3除余2且被5除余3的數按照從小到大的順序排成一列,構成一個數列,則該數列的項數是( )
A.135B.134C.59D.58
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】天上有些恒星的亮度是會變化的,其中一種稱為造父(型)變星,本身體積會膨脹收縮造成亮度周期性的變化.第一顆被描述的經典造父變星是在1784年.
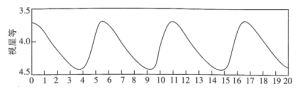
上圖為一造父變星的亮度隨時間的周期變化圖,其中視星等的數值越小,亮度越高,則此變星亮度變化的周期、最亮時視星等,分別約是( )
A.5.5,3.7B.5.4,4.4C.6.5,3.7D.5.5,4.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() :
:![]() .
.
(1)曲線![]() :
:![]() 與
與![]() 相交于
相交于![]() ,
,![]() 兩點,
兩點,![]() 為
為![]() 上異于
上異于![]() ,
,![]() 的點,若直線
的點,若直線![]() 的斜率為1,求直線
的斜率為1,求直線![]() 的斜率;
的斜率;
(2)若![]() 的左焦點為
的左焦點為![]() ,右頂點為
,右頂點為![]() ,直線
,直線![]() :
:![]() .過
.過![]() 的直線
的直線![]() 與
與![]() 相交于
相交于![]() ,
,![]() (
(![]() 在第一象限)兩點,與
在第一象限)兩點,與![]() 相交于
相交于![]() ,是否存在
,是否存在![]() 使
使![]() 的面積等于
的面積等于![]() 的面積與
的面積與![]() 的面積之和.若存在,求直線
的面積之和.若存在,求直線![]() 的方程;若不存在,請說明理由.
的方程;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 上一點
上一點![]() 到其焦點下的距離為10.
到其焦點下的距離為10.
(1)求拋物線C的方程;
(2)設過焦點F的的直線![]() 與拋物線C交于
與拋物線C交于![]() 兩點,且拋物線在
兩點,且拋物線在![]() 兩點處的切線分別交x軸于
兩點處的切線分別交x軸于![]() 兩點,求
兩點,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】近年來,我國經濟取得了長足的進步,同時性別比例問題日益突出.根據國家統計局發布的2019年統計年鑒,將國家31個省級行政區(特別行政區未記人)的人均國內生產總值與人口性別比例(每100位女性所對應的男性數目)做出了如下柱狀圖.從人口統計學角度來說,性別比例正常范圍在102至107之間.人均國內生產總值小于6.5萬元人民幣(約1萬美元)稱為欠發達地區,大于或等于6.5萬元的地區稱為發達地區.
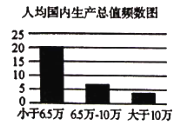
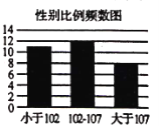
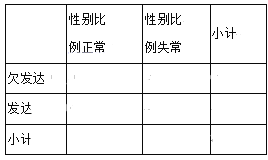
(1)已知性別比例正常的省級行政區中欠發達的行政區的個數是發達行政區的兩倍,完成列聯表,并判斷是否有90%的把握認為各省級行政區的性別比例與經濟發展程度有關;
(2)在人均國內生產總值介于6.5萬與10萬之間的7省級行政區中,有3個人口性別比例正常,從中任取兩個,求抽到兩個省級行政區的人口性別比例都正常的概率.
附:參考公式及臨界值表
 ,
,![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】F是拋物線![]() 的焦點,M是拋物線C上位于第一象限內的任意一點,過
的焦點,M是拋物線C上位于第一象限內的任意一點,過![]() 三點的圓的圓心為Q,點Q到拋物線C的準線的距離為
三點的圓的圓心為Q,點Q到拋物線C的準線的距離為![]() .
.
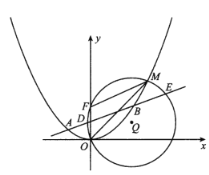
(1)求拋物線C的方程;
(2)若點M的橫坐標為![]() ,直線
,直線![]() 與拋物線C有兩個不同的交點A,B,l與圓Q有兩個不同的交點D,E,求當
與拋物線C有兩個不同的交點A,B,l與圓Q有兩個不同的交點D,E,求當![]() 時,
時,![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com