
【題目】為調查中國及美國的高中生在“家”、“朋友聚集的地方”、“個人空間”這三個場所中感到最幸福的場所是哪個,從中國某城市的高中生中隨機抽取了55人,從美國某城市高中生中隨機抽取了45人進行答題。中國高中生的答題情況:選擇“家”的高中生的人數占![]() ,選擇“朋友聚集的地方”的高中生的人數占
,選擇“朋友聚集的地方”的高中生的人數占![]() ,選擇“個人空間”的高中生的人數占
,選擇“個人空間”的高中生的人數占![]() ,美國高中生的答題情況:選擇“家”的高中生的人數占
,美國高中生的答題情況:選擇“家”的高中生的人數占![]() ,選擇“朋友聚集的地方”的高中生的人數占
,選擇“朋友聚集的地方”的高中生的人數占![]() ,選擇“個人空間”的高中生的人數占
,選擇“個人空間”的高中生的人數占![]() 。
。
(1)請根據以上調查結果將下面的2X2列聯表補充完整,并判斷能否有95%的把握認為戀家(在家里感到最幸福)與國別有關;
在家里感到最幸福 | 在其他場所感到最幸福 | 總計 | |
中國高中生 | |||
美國高中生 | |||
總計 |
(2)從被調查的不“戀家”的美國高中生中,用分層抽樣的方法隨機選出4人接受進一步調查,再從4人中隨機選出2人到中國交流學習,求2人中含有在“個人空間”感到最幸福的高中生的概率。
| 0.050 | 0.025 | 0.010 | 0.001 |
| 3.841 | 5.024 | 6.635 | 10.8 |
附:
【答案】(1)有95%的把握認為戀家與國別有關(2)p=![]()
【解析】
(1)根據題意填寫列聯表,計算觀測值,對照臨界值,即可得出結論;
(2)根據分層抽樣原理,利用列舉法求出基本事件的件數,計算所求的概率值.
(1)由題意,中國高中生的答題情況:選擇“家”的高中生的人數為![]() 人,則選擇“其他場所”的高中生的人數為
人,則選擇“其他場所”的高中生的人數為![]() 人,美國高中生的答題情況:選擇“家”的高中生的人數為
人,美國高中生的答題情況:選擇“家”的高中生的人數為![]() 人,則選擇“其他場所”的高中生的人數占
人,則選擇“其他場所”的高中生的人數占![]() 人,可得
人,可得![]() 的列表:
的列表:
在家里感到最幸福 | 在其他場所感到最幸福 | 總計 | |
中國高中生 | 22 | 33 | 55 |
美國高中生 | 9 | 4 | 45 |
總計 | 31 | 69 | 100 |
所以![]() ,
,
所以有95%的把握認為“戀家”與國別有關.
(2)用分層抽樣的方法抽取4人,從被調查的不“戀家”的美國高中生中選出4人,其中含有在“個人空間”的有1人,分別設為![]() ,
,
從中抽取2人,共有:![]() ,共有6種抽法,
,共有6種抽法,
其中含有“個人空間”共有:![]() ,共有3種,
,共有3種,
所以2人中含有在“個人空間”感到最幸福的高中生的概率為![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
【題目】已知梯形![]() 如圖(1)所示,其中
如圖(1)所示,其中![]() ,
, ![]() ,四邊形
,四邊形![]() 是邊長為
是邊長為![]() 的正方形,現沿
的正方形,現沿![]() 進行折疊,使得平面
進行折疊,使得平面![]() 平面
平面![]() ,得到如圖(2)所示的幾何體.
,得到如圖(2)所示的幾何體.

(Ⅰ)求證:平面![]() 平面
平面![]() ;
;
(Ⅱ)已知點![]() 在線段
在線段![]() 上,且
上,且![]() 平面
平面![]() ,求
,求![]() 與平面
與平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某保險公司對一個擁有20000人的企業推出一款意外險產品,每年每位職工只要交少量保費,發生意外后可一次性獲得若干賠償金,保險公司把企業的所有崗位共分為![]() 三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
三類工種,從事這三類工種的人數分別為12000,6000,2000,由歷史數據統計出三類工種的賠付頻率如下表(并以此估計賠付概率):
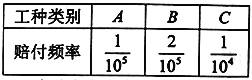
已知![]() 三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
三類工種職工每人每年保費分別為25元、25元、40元,出險后的賠償金額分別為100萬元、100萬元、50萬元,保險公司在開展此項業務過程中的固定支出為每年10萬元.
(1)求保險公司在該業務所或利潤的期望值;
(2)現有如下兩個方案供企業選擇:
方案1:企業不與保險公司合作,職工不交保險,出意外企業自行拿出與保險公司提供的等額賠償金賠償付給意外職工,企業開展這項工作的固定支出為每年12萬元;
方案2:企業與保險公司合作,企業負責職工保費的70%,職工個人負責保費的30%,出險后賠償金由保險公司賠付,企業無額外專項開支.
請根據企業成本差異給出選擇合適方案的建議.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在正四棱臺![]() 中,上底面邊長為4,下底面邊長為8,高為5,點
中,上底面邊長為4,下底面邊長為8,高為5,點![]() 分別在
分別在![]() 上,且
上,且![]() .過點
.過點![]() 的平面
的平面![]() 與此四棱臺的下底面會相交,則平面
與此四棱臺的下底面會相交,則平面![]() 與四棱臺的面的交線所圍成圖形的面積的最大值為
與四棱臺的面的交線所圍成圖形的面積的最大值為

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知二次函數f(x)=x2-(2m+1)x+m.
(1)若方程f(x)=0有兩個不等的實根x1,x2,且-1<x1<0<x2<1,求m的取值范圍;
(2)若對任意的x∈[1,2],![]() ≤2恒成立,求m的取值范圍.
≤2恒成立,求m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知中心在原點,焦點在![]() 軸上的橢圓
軸上的橢圓![]() 的離心率為
的離心率為![]() ,過左焦點
,過左焦點![]() 且垂直于
且垂直于![]() 軸的直線交橢圓
軸的直線交橢圓![]() 于
于![]() 兩點,且
兩點,且![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)若直線![]() 是圓
是圓![]() 上的點
上的點![]() 處的切線,點
處的切線,點![]() 是直線
是直線![]() 上任一點,過點
上任一點,過點![]() 作橢圓
作橢圓![]() 的切線
的切線![]() ,切點分別為
,切點分別為![]() ,設切線的斜率都存在.求證:直線
,設切線的斜率都存在.求證:直線![]() 過定點,并求出該定點的坐標.
過定點,并求出該定點的坐標.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是橢圓
是橢圓![]() :
:![]() (
(![]() )與拋物線
)與拋物線![]() :
:![]() 的一個公共點,且橢圓與拋物線具有一個相同的焦點
的一個公共點,且橢圓與拋物線具有一個相同的焦點![]() .
.
(Ⅰ)求橢圓![]() 及拋物線
及拋物線![]() 的方程;
的方程;
(Ⅱ)設過![]() 且互相垂直的兩動直線
且互相垂直的兩動直線![]() ,
,![]() 與橢圓
與橢圓![]() 交于
交于![]() 兩點,
兩點,![]() 與拋物線
與拋物線![]() 交于
交于![]() 兩點,求四邊形
兩點,求四邊形![]() 面積的最小值.
面積的最小值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com