Question

（19）已知是函數(shù)的一個極值點，其中，

（I）求與的關系式；

（II）求的單調區(qū)間；

（III）當時，函數(shù)的圖象上任意一點的切線斜率恒大于3，求的取值范圍.

Answer 1

19. (I)解

因為是函數(shù)的一個極值點,所以,即，

所以

（II）由（I）知，=.

當時，有，當變化時，與的變化如下表：

				1
		0		0
	單調遞減	極小值	單調遞增	極大值	單調遞減

由上表知，當時，在單調遞減，在單調遞增，在上單調遞減.

（III）解法一：

由已知，得，即

∵，

∴

即      （*）

設，其函數(shù)圖象的開口向上，

由題意（*）式恒成立，∴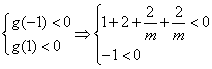

                   

                   ∴ .

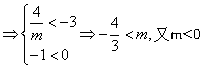
即的取值范圍為

解法二：由已知，得，即，

∵，

      ∴      （*）

     1*    x=1時，（*）式化為0<1恒成立，∴。

     2*    x≠1時，∵

                    （*）式化為,

   令t= x－1，則t∈[－2,0]，記g(t)=t－,

    則g(t)在區(qū)間[－2,0]是單調增函數(shù)。

∴g(t)_min=g(－2)=

     由（*）式恒成立，必有又m<0，

∴

綜上1*、2*知