
【題目】一小袋中有3個紅色、3個白色的乒乓球(其體積、質地完全相同),從袋中隨機摸出3個球.
(1)求摸出的3個球都為白球的概率是多少?
(2)求摸出的3個球為2個紅球、1個白球的概率是多少?
【答案】(1)![]() (2)
(2)![]()
【解析】
先利用列舉法求得試驗所包含的基本事件的個數,
(1)找出事件![]() {摸出的3個球為白球}所包含的基本的事件的個數,利用古典概型的概率計算公式,即可求解;
{摸出的3個球為白球}所包含的基本的事件的個數,利用古典概型的概率計算公式,即可求解;
(2)找出事件![]() {摸出的3個球為2個紅球、1個白球}所包含的基本的事件的個數,利用古典概型的概率計算公式,即可求解.
{摸出的3個球為2個紅球、1個白球}所包含的基本的事件的個數,利用古典概型的概率計算公式,即可求解.
由題意,把3個紅色乒乓球標記為![]() ,
,![]() ,
,![]() ,3個白色乒乓球標記為1,2,3,
,3個白色乒乓球標記為1,2,3,
從6個球中隨機摸出3個球的樣本點為![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,123,共20個基本事件.
,123,共20個基本事件.
(1)記事件![]() {摸出的3個球為白球},事件
{摸出的3個球為白球},事件![]() 包含的樣本點1個,即123,則
包含的樣本點1個,即123,則![]() .
.
(2)記事件![]() {摸出的3個球為2個紅球、1個白球},
{摸出的3個球為2個紅球、1個白球},
則事件![]() 包含
包含![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,共有9個基本事件,所以概率為
,共有9個基本事件,所以概率為![]() .
.


科目:高中數學 來源: 題型:
【題目】平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系.且曲線
軸的正半軸為極軸建立極坐標系.且曲線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求直線![]() 的普通方程以及曲線
的普通方程以及曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)若點![]() 的極坐標為
的極坐標為![]() ,直線
,直線![]() 與曲線
與曲線![]() 交于
交于![]() 兩點,求
兩點,求![]() 的值
的值
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】秉持“綠水青山就是金山銀山”的生態文明發展理念,為推動新能源汽車產業迅速發展,有必要調查研究新能源汽車市場的生產與銷售.下圖是我國某地區![]() 年至
年至![]() 年新能源汽車的銷量(單位:萬臺)按季度(一年四個季度)統計制成的頻率分布直方圖.
年新能源汽車的銷量(單位:萬臺)按季度(一年四個季度)統計制成的頻率分布直方圖.
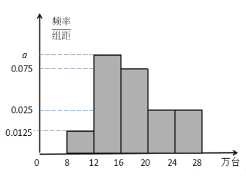
(1)求直方圖中![]() 的值,并估計銷量的中位數;
的值,并估計銷量的中位數;
(2)請根據頻率分布直方圖估計新能源汽車平均每個季度的銷售量(同一組數據用該組中間值代表),并以此預計![]() 年的銷售量.
年的銷售量.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖是某直三棱柱被削去上底后所得幾何體的左視圖、俯視圖、直觀圖,在直觀圖中,M是BD的中點,左視圖是直角梯形,俯視圖是等腰直角三角形,有關數據如圖所示.
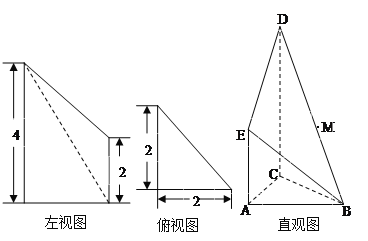
(Ⅰ)求該幾何體的表面積和體積;
(Ⅱ)求點C到平面MAB的距離.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】一位老人把他積蓄的![]() 枚金幣分給
枚金幣分給![]() 個兒女(
個兒女(![]() 、
、![]() 為大于 1 的正整數).首先, 給老大 1 枚金幣和余下的
為大于 1 的正整數).首先, 給老大 1 枚金幣和余下的![]() ;然后,從余下的金幣中給老二 2 枚金幣和余下的
;然后,從余下的金幣中給老二 2 枚金幣和余下的![]() ;依此類推 ,第幾個孩子就分幾枚金幣和余下的
;依此類推 ,第幾個孩子就分幾枚金幣和余下的![]() ,直到最小的孩子分到最后剩下的
,直到最小的孩子分到最后剩下的![]() 枚金幣.問老人分給每個孩子的金幣是否一樣多?
枚金幣.問老人分給每個孩子的金幣是否一樣多?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學校共有教師300人,其中中級教師有120人,高級教師與初級教師的人數比為![]() .為了解教師專業發展要求,現采用分層抽樣的方法進行調查,在抽取的樣本中有中級教師72人,則該樣本中的高級教師人數為__________.
.為了解教師專業發展要求,現采用分層抽樣的方法進行調查,在抽取的樣本中有中級教師72人,則該樣本中的高級教師人數為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】目前,新冠病毒引發的肺炎疫情在全球肆虐,為了解新冠肺炎傳播途徑,采取有效防控措施,某醫院組織專家統計了該地區500名患者新冠病毒潛伏期的相關信息,數據經過匯總整理得到如圖所示的頻率分布直方圖(用頻率作為概率).潛伏期不高于平均數的患者,稱為“短潛伏者”,潛伏期高于平均數的患者,稱為“長潛伏者”.

(1)求這500名患者潛伏期的平均數(同一組中的數據用該組區間的中點值作代表),并計算出這500名患者中“長潛伏者”的人數;
(2)為研究潛伏期與患者年齡的關系,以潛伏期是否高于平均數為標準進行分層抽樣,從上述500名患者中抽取300人,得到如下表格.
(i)請將表格補充完整;
短潛伏者 | 長潛伏者 | 合計 | |
60歲及以上 | 90 | ||
60歲以下 | 140 | ||
合計 | 300 |
(ii)研究發現,某藥物對新冠病毒有一定的抑制作用,現需在樣本中60歲以下的140名患者中按分層抽樣方法抽取7人做I期臨床試驗,再從選取的7人中隨機抽取兩人做Ⅱ期臨床試驗,求兩人中恰有1人為“長潛伏者”的概率.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com