f(x)是以2為周期的偶函數,且當x∈[0,1]時,f(x)=x,若在區間[-1,3]內,函數g(x)=f(x)-kx-k有4個零點,則實數k的取值范圍是 .
【答案】
分析:根據函數是一個偶函數且周期是2,寫出函數在[-1,0],[2,3],[-1,0)上的函數解析式,根據g(x)仍為一次函數,有4個零點,故在四段內各有一個零點.分別在這四段上討論零點的情況,零點的范圍,最后求出幾種結果的交集.
解答:解:x在[0,1],f(x)=x 由于f(x)是偶函數,x在[-1,0],f(x)=-x f(x)是周期為2的函數 f(2)=f(0)=0 函數解析式:y=-x+2 x在[2,3]時,函數解析式:y=x-2 g(x)仍為一次函數,有4個零點,故在四段內各有一個零點. x在[-1,0) g(x)=-x-kx-k=-(k+1)x-k 令g(x)=0 x=-
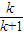
-1≤-
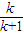
<0
解得k>0 x在(0,1]g(x)=x-kx-k=(1-k)x-k 令g(x)=0 x=
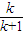
0<
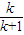
≤1 解的0<k≤

x在(1,2]g(x)=-x+2-kx-k=-(k+1)x+2-k 令g(x)=0 x=
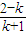
1<
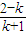
≤2 解的0≤k<

x在(2,3]g(x)=x-2-kx-k=(1-k)x-2-k 令g(x)=0 x=
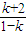
2<
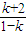
≤3 解的0<k≤

綜上可知,k的取值范圍為:0<k≤

故答案為:(0,

].
點評:學生知識經驗已較為豐富,智力發展已到了形式運演階段,具備了較強的抽象思維能力和演繹推理能力,所以本題符合這類學生的心理發展特點,從而促進思維能力的進一步發展.

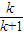
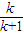 <0
<0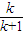
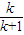 ≤1 解的0<k≤
≤1 解的0<k≤ x在(1,2]g(x)=-x+2-kx-k=-(k+1)x+2-k 令g(x)=0 x=
x在(1,2]g(x)=-x+2-kx-k=-(k+1)x+2-k 令g(x)=0 x=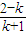
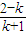 ≤2 解的0≤k<
≤2 解的0≤k<
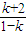
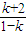 ≤3 解的0<k≤
≤3 解的0<k≤ 綜上可知,k的取值范圍為:0<k≤
綜上可知,k的取值范圍為:0<k≤
 ].
].
