
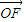 =(c,0)(c>0),
=(c,0)(c>0),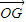 =(n,n)(n∈R),|
=(n,n)(n∈R),|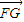 |的最小值為1,若動點P同時滿足下列三個條件:
|的最小值為1,若動點P同時滿足下列三個條件: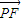 |=
|=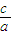 |
|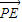 |(a>c>0);
|(a>c>0);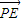 =λ
=λ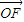 (其中
(其中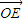 =(
=(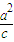 ,t),λ≠0,t∈R);
,t),λ≠0,t∈R);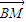 |=|
|=|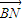 |?若存在,求出k的范圍;若不存在,請說明理由.
|?若存在,求出k的范圍;若不存在,請說明理由.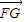 |=
|=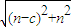 =
=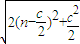 ,利用二次函數的性質得出其最小值,從而求得c值.
,利用二次函數的性質得出其最小值,從而求得c值.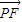 |=
|=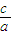 |
|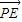 |(a>c>0).從而得出點P在以F為焦點,x=
|(a>c>0).從而得出點P在以F為焦點,x=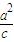 為準線的橢圓上,從而
為準線的橢圓上,從而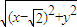 =
=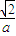 |
|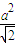 -x|,最后將點B(0-1)代入,解得a即可寫出曲線C的方程;
-x|,最后將點B(0-1)代入,解得a即可寫出曲線C的方程;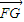 |=
|=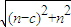 =
=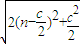 ,
,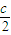 時,|
時,|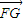 |min=
|min=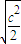 =1,所以c=
=1,所以c=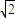 .(3分)
.(3分)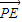 =λ
=λ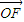 (λ≠0),∴PE⊥直線x=
(λ≠0),∴PE⊥直線x=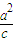 ,又|
,又|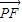 |=
|=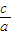 |
|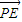 |(a>c>0).
|(a>c>0).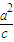 為準線的橢圓上.(5分)
為準線的橢圓上.(5分)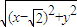 =
=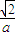 |
|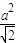 -x|,點B(0-1)代入,解得a=
-x|,點B(0-1)代入,解得a=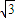 .
.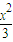 +y2=1 (7分)
+y2=1 (7分)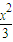 +y2=1聯立,消去y得(1+3k2)x2+6kmx+3m2-3=0.(10分)
+y2=1聯立,消去y得(1+3k2)x2+6kmx+3m2-3=0.(10分)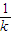 ,可得到m=
,可得到m=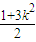 ②
②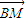 |=|
|=|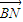 |.(14分)z
|.(14分)z

科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知直線x-2y+2=0經過橢圓C:
已知直線x-2y+2=0經過橢圓C:| x2 |
| a2 |
| y2 |
| b2 |
| 10 |
| 3 |
| 1 |
| 5 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| OF |
| OG |
| FG |
| PF |
| c |
| a |
| PE |
| PE |
| OF |
| OE |
| a2 |
| c |
| BM |
| BN |
查看答案和解析>>
科目:高中數學 來源:2011-2012學年江西省高三第一次統考理科數學 題型:解答題
已知橢圓C: +
+ =1(a>b>0),直線y=x+
=1(a>b>0),直線y=x+ 與以原點為圓心,以橢圓C的短半軸長為半徑
與以原點為圓心,以橢圓C的短半軸長為半徑
的圓相切,F1,F2為其左、右焦點,P為橢圓C上任一點,△F1PF2的重心為G,內心為I,且IG∥F1F2。⑴
求橢圓C的方程。⑵若直線L:y=kx+m(k≠0)與橢圓C交于不同兩點A,B且線段AB的垂直平分線過定點
C( ,0)求實數k的取值范圍。
,0)求實數k的取值范圍。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com