
【題目】已知口袋里裝有4個大小相同的小球,其中兩個標有數字1,兩個標有數字2.
(1)從口袋里任意取一球,求取到標有數字2的球的概率;
(2)第一次從口袋里任意取一球,放回口袋里后第二次再任意取一球,記第一次與第二次取到小球上的數字之和為![]() .當
.當![]() 為何值時,其發生的概率最大?說明理由.
為何值時,其發生的概率最大?說明理由.
【答案】(1)![]() ;(2)數字和為3時概率最大,理由詳見解析.
;(2)數字和為3時概率最大,理由詳見解析.
【解析】
(1)利用古典概型的概率計算公式即可求解.
(2)設標號為1的球為![]() ,
,![]() ,標號為2的球為
,標號為2的球為![]() ,
,![]() ,采用列舉法求出所有基本事件個數,然后分別求出數字和為2、3、4的基本事件個數,利用古典概型的概率計算公式求出各自的概率即可求解.
,采用列舉法求出所有基本事件個數,然后分別求出數字和為2、3、4的基本事件個數,利用古典概型的概率計算公式求出各自的概率即可求解.
解:(1)4個球中標有數字2的球有2個,故所求概率為![]() ,
,
(2)設標號為1的球為![]() ,
,![]() ,標號為2的球為
,標號為2的球為![]() ,
,![]() .
.
所有基本事件包括:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,共16種.
,共16種.
設事件![]() 表示數字和為2,
表示數字和為2,
包括:![]() ,
,![]() ,
,![]() ,
,![]() ,共4種,
,共4種,
故有![]() .
.
設事件![]() 表示數字和為3,
表示數字和為3,
包括:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,共8種,
,共8種,![]() .
.
設事件![]() 表示數字和為4,
表示數字和為4,
包括:![]() ,
,![]() ,
,![]() ,
,![]() ,共4種,
,共4種,
故![]() .
.
![]() 數字和為3時概率最大.
數字和為3時概率最大.


科目:高中數學 來源: 題型:
【題目】已知函數![]() ,給出以下四個命題:
,給出以下四個命題:
①![]() 的圖象關于
的圖象關于![]() 軸對稱;
軸對稱;
②![]() 在
在![]() 上是減函數;
上是減函數;
③![]() 是周期函數;
是周期函數;
④![]() 在
在![]() 上恰有兩個零點.
上恰有兩個零點.
其中真命題的序號是______.(請寫出所有真命題的序號)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() ,曲線
,曲線![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,以
為極點,以![]() 軸的正半軸為極軸建立極坐標系.
軸的正半軸為極軸建立極坐標系.
(1)求![]() 的極坐標方程;
的極坐標方程;
(2)射線![]() 的極坐標方程為
的極坐標方程為![]() ,若
,若![]() 分別與
分別與![]() 交于異于極點的
交于異于極點的![]() 兩點,求
兩點,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某水果批發商經銷某種水果(以下簡稱![]() 水果),購入價為300元/袋,并以360元/袋的價格售出,若前8小時內所購進的
水果),購入價為300元/袋,并以360元/袋的價格售出,若前8小時內所購進的![]() 水果沒有售完,則批發商將沒售完的
水果沒有售完,則批發商將沒售完的![]() 水果以220元/袋的價格低價處理完畢(根據經驗,2小時內完全能夠把
水果以220元/袋的價格低價處理完畢(根據經驗,2小時內完全能夠把![]() 水果低價處理完,且當天不再購入).該水果批發商根據往年的銷量,統計了100天
水果低價處理完,且當天不再購入).該水果批發商根據往年的銷量,統計了100天![]() 水果在每天的前8小時內的銷售量,制成如下頻數分布條形圖.
水果在每天的前8小時內的銷售量,制成如下頻數分布條形圖.
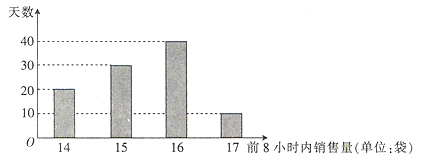
記![]() 表示
表示![]() 水果一天前8小時內的銷售量,
水果一天前8小時內的銷售量,![]() 表示水果批發商一天經營
表示水果批發商一天經營![]() 水果的利潤,
水果的利潤,![]() 表示水果批發商一天批發
表示水果批發商一天批發![]() 水果的袋數.
水果的袋數.
(1)若![]() ,求
,求![]() 與
與![]() 的函數解析式;
的函數解析式;
(2)假設這100天中水果批發商每天購入![]() 水果15袋或者16袋,分別計算該水果批發商這100天經營
水果15袋或者16袋,分別計算該水果批發商這100天經營![]() 水果的利潤的平均數,以此作為決策依據,每天應購入
水果的利潤的平均數,以此作為決策依據,每天應購入![]() 水果15袋還是16袋?
水果15袋還是16袋?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】2019年春節前后,中國爆發新型冠狀病毒(SARS-Cov-2)如圖所示為1月24日至2月16日中國內地(除湖北以外的)感染新型冠狀病毒新增人數的折線圖,為了預測分析數據的變化規律,建立了![]() 與時間變量
與時間變量![]() 的不同時間段的兩個線性回歸模型.根據1月24日至2月3日的數據(時間變量
的不同時間段的兩個線性回歸模型.根據1月24日至2月3日的數據(時間變量![]() 的值依次為1,2,3,4,5,6,7,8,9,10,11)建立模型①:
的值依次為1,2,3,4,5,6,7,8,9,10,11)建立模型①:![]() ;根據2月4日至2月16日的數據(時間變量
;根據2月4日至2月16日的數據(時間變量![]() 的值依次為12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:
的值依次為12,13,14,15,16,17,18,19,20,21,22,23,24)建立模型②:![]() .
.
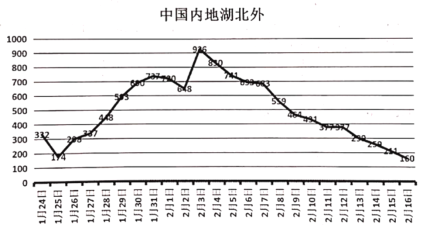
1月 24日 | 1月 25日 | 1月 26日 | 1月 27日 | 1月 28日 | 1月 29日 | 1月 30日 | 1月 31日 | 2月 1日 | 2月 2日 | 2月 3日 |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
332 | 174 | 298 | 337 | 448 | 593 | 690 | 737 | 720 | 648 | 926 |
2月 4日 | 2月 5日 | 2月 6日 | 2月 7日 | 2月 8日 | 2月 9日 | 2月 10日 | 2月 11日 | 2月 12日 | 2月 13日 | 2月 14日 | 2月 15日 | 2月 16日 |
12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
830 | 741 | 693 | 683 | 559 | 464 | 431 | 377 | 377 | 299 | 259 | 211 | 160 |
(1)求出兩個回歸直線方程;(計算結果取整數)
(2)中國政府為了人民的生命安全,聽取專家意見,了解了病毒信息,并迅速做出一系列的隔離防護措施,但新冠狀病毒在世界范圍內爆發時,某些歐美國家采取放任的態度,不治療、不隔離、不檢測,甚至不公布,請你用以上數據說明采取一系列措施的必要性,不采取措施的后果.
參考數據:![]() ,
,![]() ,
,![]() ,
,![]()
參考公式: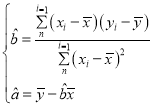 .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的離心率為
的離心率為![]() ,直線
,直線![]() 過右焦點
過右焦點![]() ,過點
,過點![]() 的直線
的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點(均不為頂點)
兩點(均不為頂點)
(1)求橢圓![]() 的方程;
的方程;
(2)已知![]() 是橢圓
是橢圓![]() 的右頂點,直線
的右頂點,直線![]() ,若直線
,若直線![]() 與直線
與直線![]() 交于點
交于點![]() 直線
直線![]() 與直線
與直線![]() 交于點
交于點![]() ,試判斷
,試判斷![]() 是否為定值,若是,求出定值,若不是請說明理由.
是否為定值,若是,求出定值,若不是請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知橢圓![]() 的焦距為4.且過點
的焦距為4.且過點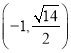 .
.
(1)求橢圓E的方程;
(2)設![]() ,
,![]() ,
,![]() ,過B點且斜率為
,過B點且斜率為![]() 的直線l交橢圓E于另一點M,交x軸于點Q,直線AM與直線
的直線l交橢圓E于另一點M,交x軸于點Q,直線AM與直線![]() 相交于點P.證明:
相交于點P.證明:![]() (O為坐標原點).
(O為坐標原點).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在棱長為1的正方體![]() 中,E,F分別為線段CD和
中,E,F分別為線段CD和![]() 上的動點,且滿足
上的動點,且滿足![]() ,則四邊形
,則四邊形![]() 所圍成的圖形(如圖所示陰影部分)分別在該正方體有公共頂點的三個面上的正投影的面積之和( )
所圍成的圖形(如圖所示陰影部分)分別在該正方體有公共頂點的三個面上的正投影的面積之和( )

A. 有最小值![]() B. 有最大值
B. 有最大值![]() C. 為定值3D. 為定值2
C. 為定值3D. 為定值2
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com