
已知數列 的首項
的首項 其中
其中 ,
, 令集合
令集合 .
.
(Ⅰ)若 是數列
是數列 中首次為1的項,請寫出所有這樣數列的前三項;
中首次為1的項,請寫出所有這樣數列的前三項;
(Ⅱ)求證: ;
;
(Ⅲ)當 時,求集合
時,求集合 中元素個數
中元素個數 的最大值.
的最大值.
(Ⅰ)27,9,3;8,9,3;6,2,3..(Ⅱ)見解析. (Ⅲ)集合 重元素個數
重元素個數 的最大值為21.
的最大值為21.
解析試題分析:(Ⅰ)依次代入寫出27,9,3;8,9,3;6,2,3.
(Ⅱ)根據 及
及 須討論
須討論 被3除余1,,
被3除余1,, 被3除余2,
被3除余2, 被3除余0,等三種情況.
被3除余0,等三種情況.
(Ⅲ)注意由已知遞推關系推得數列 滿足:
滿足:
當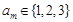 時,總有
時,總有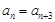 成立,其中
成立,其中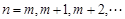 .
.
因此應注意討論當 時,數列
時,數列 中大于3的各項:
中大于3的各項:
按逆序排列各項,構成的數列記為 ,由(Ⅰ)可得
,由(Ⅰ)可得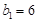 或9,
或9,
由(Ⅱ)的證明過程即可知數列 的項滿足:
的項滿足: ,且當
,且當 是3的倍數時,若使
是3的倍數時,若使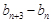 最小,需使
最小,需使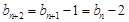 ,
,
滿足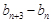 最小的數列
最小的數列 中,
中,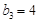 或7,且
或7,且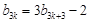 ,
,
得到數列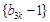 是首項為
是首項為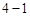 或
或 的公比為3的等比數列,應用等比數列的通項公式即可得出結論.
的公比為3的等比數列,應用等比數列的通項公式即可得出結論.
解答本題的關鍵是注意“轉化”成等比數列問題.
試題解析:(Ⅰ)27,9,3;8,9,3;6,2,3. 3分
(Ⅱ)若 被3除余1,則由已知可得
被3除余1,則由已知可得 ,
,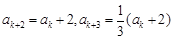 ;
;
若 被3除余2,則由已知可得
被3除余2,則由已知可得 ,
,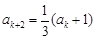 ,
, ;
;
若 被3除余0,則由已知可得
被3除余0,則由已知可得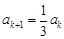 ,
,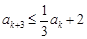 ;
;
所以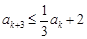 ,
,
所以
所以,對于數列 中的任意一項
中的任意一項 ,“若
,“若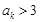 ,則
,則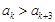 ”.
”.
因為 ,所以
,所以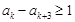 .
.
所以數列 中必存在某一項
中必存在某一項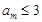 (否則會與上述結論矛盾!)
(否則會與上述結論矛盾!)
若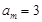 ,則
,則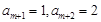 ;若
;若 ,則
,則 ,若
,若 ,則
,則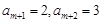 ,
,
由遞推關系易得 . 8分
. 8分
(Ⅲ)集合 中元素個數
中元素個數 的最大值為21.
的最大值為21.
由已知遞推關系可推得數列 滿足:
滿足:
當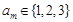 時,總有
時,總有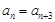 成立,其中
成立,其中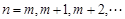 .
.
下面考慮當 時,數列
時,數列 中大于3的各項:
中大于3的各項:
按逆序排列各項,構成的數列記為 ,由(I)可得
,由(I)可得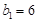 或9,
或9,
由(Ⅱ)的證明過程可知數列 的項滿足:
的項滿足: ,且當
,且當 是3的倍數時,若使
是3的倍數時,若使

 小學學習好幫手系列答案
小學學習好幫手系列答案 小學同步三練核心密卷系列答案
小學同步三練核心密卷系列答案科目:高中數學 來源: 題型:解答題
數列{an}的前n項和記為Sn,a1=t,點(Sn,an+1)在直線y=2x+1上,n∈N*.
(1)當實數t為何值時,數列{an}是等比數列?
(2)在(1)的結論下,設bn=log3an+1,Tn是數列 的前n項和, 求T2 013的值.
的前n項和, 求T2 013的值.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知點(1,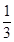 )是函數
)是函數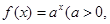 且
且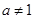 )的圖象上一點,等比數列
)的圖象上一點,等比數列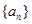 的前
的前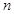 項和為
項和為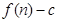 ,數列
,數列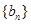
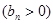 的首項為
的首項為 ,且前
,且前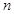 項和
項和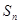 滿足
滿足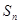 -
-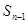 =
=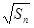 +
+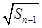 (
(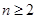 ).
).
(1)求數列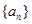 和
和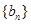 的通項公式;
的通項公式;
(2)求數列{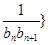 前
前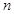 項和為
項和為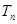 ,問
,問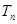 >
>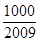 的最小正整數
的最小正整數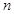 是多少?
是多少?
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
各項均為正數的等比數列{an}中,已知a2="8," a4="128," bn=log2an .
(1)求數列{an}的通項公式;
(2)求數列{bn}的前n項和Sn
(3)求滿足不等式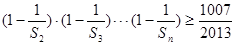 的正整數n的最大值
的正整數n的最大值
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com