
【題目】設數列{an}滿足an+1=an2﹣an+1(n∈N*),Sn為{an}的前n項和.證明:對任意n∈N* ,
(I)當0≤a1≤1時,0≤an≤1;
(II)當a1>1時,an>(a1﹣1)a1n﹣1;
(III)當a1= ![]() 時,n﹣
時,n﹣ ![]() <Sn<n.
<Sn<n.
【答案】證明:(Ⅰ)用數學歸納法證明. ①當n=1時,0≤an≤1成立.
②假設當n=k(k∈N*)時,0≤ak≤1,
則當n=k+1時, ![]() =(
=( ![]() )2+
)2+ ![]() ∈[
∈[ ![]() ][0,1],
][0,1],
由①②知, ![]() .
.
∴當0≤a1≤1時,0≤an≤1.
(Ⅱ)由an+1﹣an=( ![]() )﹣an=(an﹣1)2≥0,知an+1≥an .
)﹣an=(an﹣1)2≥0,知an+1≥an .
若a1>1,則an>1,(n∈N*),
從而 ![]() =
= ![]() ﹣an=an(an﹣1),
﹣an=an(an﹣1),
即 ![]() =an≥a1 ,
=an≥a1 ,
∴ ![]() ,
,
∴當a1>1時,an>(a1﹣1)a1n﹣1 .
(Ⅲ)當 ![]() 時,由(Ⅰ),0<an<1(n∈N*),故Sn<n,
時,由(Ⅰ),0<an<1(n∈N*),故Sn<n,
令bn=1﹣an(n∈N*),由(Ⅰ)(Ⅱ),bn>bn+1>0,(n∈N*),
由 ![]() ,得
,得 ![]() .
.
∴ ![]() =(b1﹣b2)+(b2﹣b3)+…+(bn﹣bn+1)=b1﹣bn+1<b1=
=(b1﹣b2)+(b2﹣b3)+…+(bn﹣bn+1)=b1﹣bn+1<b1= ![]() ,
,
∵ ![]() ≥
≥ ![]() ,
,
∴nbn2![]() ,即
,即 ![]() ,(n∈N*),
,(n∈N*),
∵ ![]() =
= ![]() =
= ![]() ,
,
∴b1+b2+…+bn![]() [(
[( ![]() )+(
)+( ![]() )+…+(
)+…+( ![]() )]=
)]= ![]() ,
,
即n﹣Sn![]() ,亦即
,亦即 ![]() ,
,
∴當 ![]() 時,
時, ![]() .
.
【解析】(Ⅰ)用數學歸納法能證明當0≤a1≤1時,0≤an≤1.(Ⅱ)由an+1﹣an=( ![]() )﹣an=(an﹣1)2≥0,知an+1≥an . 從而
)﹣an=(an﹣1)2≥0,知an+1≥an . 從而 ![]() =an≥a1 , 由此能證明當a1>1時,an>(a1﹣1)a1n﹣1 . (Ⅲ)當
=an≥a1 , 由此能證明當a1>1時,an>(a1﹣1)a1n﹣1 . (Ⅲ)當 ![]() 時,Sn<n,令bn=1﹣an(n∈N*),則bn>bn+1>0,(n∈N*),由
時,Sn<n,令bn=1﹣an(n∈N*),則bn>bn+1>0,(n∈N*),由 ![]() ,得
,得 ![]() .從而
.從而 ![]() ,(n∈N*),由此能證明當
,(n∈N*),由此能證明當 ![]() 時,
時, ![]() .
.
【考點精析】解答此題的關鍵在于理解數列的前n項和的相關知識,掌握數列{an}的前n項和sn與通項an的關系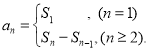 .
.


科目:高中數學 來源: 題型:
【題目】設樣本數據x1 , x2 , …,x2017的方差是4,若yi=2xi﹣1(i=1,2,…,2017),則y1 , y2 , …y2017的方差為 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,在直角梯形ABCP中,CP∥AB,CP⊥CB,AB=BC= ![]() CP=2,D是CP的中點,將△PAD沿AD折起,使得PD⊥CD.
CP=2,D是CP的中點,將△PAD沿AD折起,使得PD⊥CD. 
(Ⅰ)若E是PC的中點,求證:AP∥平面BDE;
(Ⅱ)求證:平面PCD⊥平面ABCD;
(Ⅲ)求二面角A﹣PB﹣C的大小.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在如圖所示的五面體中,面ABCD為直角梯形,∠BAD=∠ADC= ![]() ,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是邊長為2的正三角形.
,平面ADE⊥平面ABCD,EF=2DC=4AB=4,△ADE是邊長為2的正三角形.
(Ⅰ)證明:BE⊥平面ACF;
(Ⅱ)求二面角A﹣BC﹣F的余弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】F是拋物線C:y2=4x的焦點,過F作兩條斜率都存在且互相垂直的直線l1 , l2 , l1交拋物線C于點A,B,l2交拋物線C于點G,H,則 ![]() 的最小值是( )
的最小值是( )
A.8
B.8 ![]()
C.16
D.16 ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在極坐標系中,已知直線l的極坐標方程 為ρsin(θ+ ![]() )=1,圓C的圓心是C(1,
)=1,圓C的圓心是C(1, ![]() ),半徑為1,求:
),半徑為1,求:
(1)圓C的極坐標方程;
(2)直線l被圓C所截得的弦長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將函數y=2sin(2x+ ![]() )的圖象向右平移
)的圖象向右平移 ![]() 個單位,所得圖象對應的函數( )
個單位,所得圖象對應的函數( )
A.在區間[ ![]() ,
, ![]() ]上單調遞增
]上單調遞增
B.在區間[ ![]() ,
, ![]() ]上單調遞減
]上單調遞減
C.在區間[﹣ ![]() ,
, ![]() ]上單調遞增
]上單調遞增
D.在區間[﹣ ![]() ,
, ![]() ]上單調遞減
]上單調遞減
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐P﹣ABCD 中,∠ABC=∠BAD=90°,BC=2AD,△PAB與△PAD 都是邊長為2的等邊三角形,E 是BC的中點.
(Ⅰ)證明:平面AE∥平面 PCD;
(Ⅱ)求PAB與平面 PCD 所成二面角的大小.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com