
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).以坐標原點
為參數).以坐標原點![]() 為極點,
為極點,![]() 軸正半軸為極軸建立極坐標系,直線
軸正半軸為極軸建立極坐標系,直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設點![]() ,若直線
,若直線![]() 與曲線
與曲線![]() 相交于
相交于![]() 、
、![]() 兩點,求
兩點,求![]() 的值
的值
 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:高中數學 來源: 題型:
【題目】我國著名的數學家秦九韶在《數書九章》提出了“三斜求積術”.他把三角形的三條邊分別稱為小斜、中斜和大斜.三斜求積術就是用小斜平方加上大斜平方,送到中斜平方,取相減后余數的一半,自乘而得一個數,小斜平方乘以大斜平方,送到上面得到的那個數,相減后余數被4除,所得的數作為“實”,1作為“隅”,開平方后即得面積.所謂“實”、“隅”指的是在方程![]() 中,p為“隅”,q為“實”.即若
中,p為“隅”,q為“實”.即若![]() 的大斜、中斜、小斜分別為a,b,c,則
的大斜、中斜、小斜分別為a,b,c,則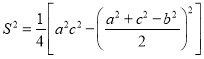 .已知點D是
.已知點D是![]() 邊AB上一點,
邊AB上一點,![]() ,
,![]() ,
,![]() ,
,![]() ,則
,則![]() 的面積為________.
的面積為________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】古人云:“腹有詩書氣自華.”為響應全民閱讀,建設書香中國,校園讀書活動的熱潮正在興起.某校為統計學生一周課外讀書的時間,從全校學生中隨機抽取![]() 名學生進行問卷調査,統計了他們一周課外讀書時間(單位:
名學生進行問卷調査,統計了他們一周課外讀書時間(單位:![]() )的數據如下:
)的數據如下:
一周課外讀書時間/ |
|
|
|
|
|
|
|
|
| 合計 |
頻數 | 4 | 6 | 10 | 12 | 14 | 24 |
| 46 | 34 |
|
頻率 | 0.02 | 0.03 | 0.05 | 0.06 | 0.07 | 0.12 | 0.25 |
| 0.17 | 1 |
(1)根據表格中提供的數據,求![]() ,
,![]() ,
,![]() 的值并估算一周課外讀書時間的中位數.
的值并估算一周課外讀書時間的中位數.
(2)如果讀書時間按![]() ,
,![]() ,
,![]() 分組,用分層抽樣的方法從
分組,用分層抽樣的方法從![]() 名學生中抽取20人.
名學生中抽取20人.
①求每層應抽取的人數;
②若從![]() ,
,![]() 中抽出的學生中再隨機選取2人,求這2人不在同一層的概率.
中抽出的學生中再隨機選取2人,求這2人不在同一層的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】袋中裝有9只球,其中標有數字1,2,3,4的小球各2個,標數字5的小球有1個.從袋中任取3個小球,每個小球被取出的可能性都相等,用![]() 表示取出的3個小球上的最大數字.
表示取出的3個小球上的最大數字.
(1)求取出的3個小球上的數字互不相同的概率;
(2)求隨機變量![]() 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某學生社團對![]() 年元宵節當天游覽磁器口古鎮景區的游客滿意度抽樣調查,從當日
年元宵節當天游覽磁器口古鎮景區的游客滿意度抽樣調查,從當日![]() 萬名游客中隨機抽取
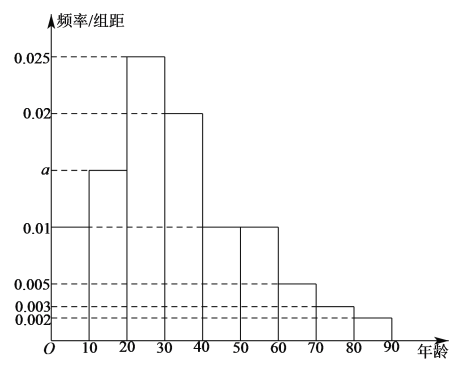
萬名游客中隨機抽取![]() 人進行統計,結果如下圖的頻率分布表和頻率分布直方圖:
人進行統計,結果如下圖的頻率分布表和頻率分布直方圖:
年齡 | 頻數 | 頻率 | 滿意 | 不滿意 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
合計 |
|
|
|
|
(1)求![]() 、
、![]() 、
、![]() 的值;
的值;
(2)利用頻率分布直方圖,估算游客的平均年齡和年齡的中位數;
(3)稱年齡不低于![]() 歲的人群為“安逸人群”,完成
歲的人群為“安逸人群”,完成![]() 列聯表,并判斷是否有
列聯表,并判斷是否有![]() 的把握認為游客的滿意度與“安逸人群”人數相關.
的把握認為游客的滿意度與“安逸人群”人數相關.
|
| 合計 | |
滿意 | |||
不滿意 | |||
合計 |
參考公式: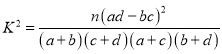 ,其中
,其中![]() .
.
參考數據:![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,直線l的參數方程為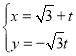 (t為參數),以坐標原點為極點,x軸正半軸為極軸,建立極坐標系,已知曲線C的極坐標方程為
(t為參數),以坐標原點為極點,x軸正半軸為極軸,建立極坐標系,已知曲線C的極坐標方程為![]() .
.
(1)求直線l的普通方程與曲線C的直角坐標方程;
(2)設點![]() ,直線l與曲線C交于不同的兩點A、B,求
,直線l與曲線C交于不同的兩點A、B,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知定義在R上的函數f(x),f′(x)是其導函數且滿足f(x)+f′(x)>2,f(1)=2![]() ,則不等式exf(x)>4+2ex的解集為_____
,則不等式exf(x)>4+2ex的解集為_____
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com