【題目】設函數
．
（1）討論
的單調性；
（2）若對任意
，都有
恒成立，求
的取值范圍．
【答案】（1）答案不唯一，見解析；（2）
或
【解析】
（1）對函數進行求導，根據
的不同取值，利用一次等式和二次不等式的解集性質進行分類討論即可；
（2）根據的不同取值，分類討論求出函數的最小值進行求解即可.
（1）
的定義域為
，
．
①當
時，
，∴在
上單調遞減，在
上單調遞增；
②當
時，
，
∴在
和上單調遞增，在
上單調遞減；
③當
時，
，∴在上單調遞增；
④當
時，
，∴在和
上單調遞增，在
上單調遞減；
⑤當
時，
，
，∴在上單調遞增，在上單調遞減．
（2）由（1）知，①當
時，在
上的最小值為
，
∴只要
，得
，解得
或；
②當時，在上的最小值為
，
∴
，即
恒成立，得；
③當時，在上單調遞減，又
，
，∴不成立，
所以滿足條件的的取值范圍是或．
科目：高中數學 來源： 題型：
【題目】2019年，海南等8省公布了高考改革綜合方案將采取“
”模式，即語文、數學、英語必考，然后考生先在物理、歷史中選擇1門，再在思想政治、地理、化學、生物中選擇2門為了更好進行生涯規劃，甲同學對高一一年來的七次考試成績進行統計分析，其中物理、歷史成績的莖葉圖如圖所示.
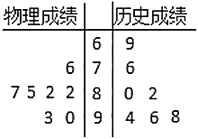
（1）若甲同學隨機選擇3門功課，求他選到物理、地理兩門功課的概率；
（2）試根據莖葉圖分析甲同學的物理和歷史哪一學科成績更穩定.（不需計算）
（3）甲同學發現，其物理考試成績
（分）與班級平均分
（分）具有線性相關關系，統計數據如下表所示，試求當班級平均分為50分時，其物理考試成績.（計算
，
時精確到0.01）
| 57 | 61 | 65 | 72 | 74 | 77 | 84 |
| 76 | 82 | 82 | 85 | 87 | 90 | 93 |
參考數據：
，
，
，
，
，
.
參考公式：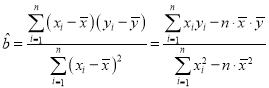
，
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在平面直角坐標系
中，曲線
的參數方程為
（
為參數）.以坐標原點
為極點，
軸正半軸為極軸建立極坐標系，直線
的極坐標方程為
.
（1）求曲線的普通方程和直線的直角坐標方程；
（2）設點
，若直線與曲線相交于
、
兩點，求
的值
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知拋物線
和圓
，傾斜角為45°的直線
過拋物線
的焦點，且與圓
相切．
（1）求
的值；
（2）動點
在拋物線的準線上，動點
在上，若在點處的切線
交
軸于點
，設
．求證點
在定直線上，并求該定直線的方程．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知橢圓
的離心率為
，短軸長為
．
（1）求橢圓
的標準方程；
（2）若橢圓的左焦點為
，過點的直線
與橢圓交于
兩點，則在
軸上是否存在一個定點
使得直線
的斜率互為相反數？若存在，求出定點的坐標；若不存在，也請說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
