
【題目】將編號為1,2,…,9的九個小球隨機放置在圓周的九個等分點上,每個等分點上各有一個小球.設圓周上所有相鄰兩球號碼之差的絕對值之和為S.求使S達到最小值的放法的概率.注:如果某種放法經旋轉或鏡面反射后可與另一種放法重合,則認為是相同的放法.
【答案】![]()
【解析】
九個編號不同的小球放在圓周的九個等分點上,每點放一個相當于九個不同元素在圓周上的一個圓形排列,共有![]() 種放法,考慮到翻轉因素,故本質不同的放法有
種放法,考慮到翻轉因素,故本質不同的放法有![]() 種.
種.
下求使S達到最小值的放法數:
在圓周上,從1到9有優弧和劣弧兩條路徑,對其中任一條路徑,設![]() 是依次排列于這段弧上的小球號碼.
是依次排列于這段弧上的小球號碼.
則![]()
當且僅當![]() 時,上式等號成立
時,上式等號成立
即每段弧上的小球編號均為由1到9遞增排列.
因此,![]() .
.
由上,知當每段弧上的球號![]() 確定之后,達到最小值的排序方案便唯一確定.
確定之后,達到最小值的排序方案便唯一確定.
在1,2,…,9中,除1與9外,剩下七個球號2,3,…,8,將它們分為兩個子集,元素較少的一個子集共有![]() 種情形,每種情形對應著圓周上使得S值達到最小的唯一排法,即有利事件總數為
種情形,每種情形對應著圓周上使得S值達到最小的唯一排法,即有利事件總數為![]() 種,故所求概率
種,故所求概率![]() .
.


科目:高中數學 來源: 題型:
【題目】已知下列說法:①對于線性回歸方程![]() ,變量
,變量![]() 增加一個單位時,
增加一個單位時,![]() 平均增加5個單位;②在線性回歸模型中,相關指數
平均增加5個單位;②在線性回歸模型中,相關指數![]() 越接近于1,則模型回歸效果越好;③兩個隨機變量的線性相關性越強,則相關系數就越接近1;④互斥事件不一定是對立事件,對立事件一定是互斥事件;⑤演繹推理是從特殊到一般的推理,它的一般模式是“三段論”.其中說法錯誤的個數為( )
越接近于1,則模型回歸效果越好;③兩個隨機變量的線性相關性越強,則相關系數就越接近1;④互斥事件不一定是對立事件,對立事件一定是互斥事件;⑤演繹推理是從特殊到一般的推理,它的一般模式是“三段論”.其中說法錯誤的個數為( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某班學生喜好體育運動是否與性別有關,對本班50人進行了問卷調查得到了如下的列聯表:
喜好體育運動 | 不喜好體育運動 | 合計 | |
男生 | 5 | ||
女生 | 10 | ||
合計 | 50 |
已知按喜好體育運動與否,采用分層抽樣法抽取容量為10的樣本,則抽到喜好體育運動的人數為6.
(1)請將上面的列聯表補充完整;
(2)能否在犯錯概率不超過![]() 的前提下認為喜好體育運動與性別有關?說明你的理由.
的前提下認為喜好體育運動與性別有關?說明你的理由.
(參考公式: ![]() )
)
臨界值表
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知直線![]() 和平面
和平面![]() :①若直線
:①若直線![]() 與平面
與平面![]() 內的無數條直線平行,則
內的無數條直線平行,則![]() ;②若直線
;②若直線![]() 與平面
與平面![]() 內的任意一條直線都不平行,則直線
內的任意一條直線都不平行,則直線![]() 和平面
和平面![]() 相交;③若
相交;③若![]() ,則直線
,則直線![]() 與平面
與平面![]() 內某些直線平行;④若
內某些直線平行;④若![]() ,則存在平面
,則存在平面![]() 內的直線
內的直線![]() ,使
,使![]() .以上結論中正確的個數為( )
.以上結論中正確的個數為( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(1)若![]() 個棱長為正整數的正方體的體積之和等于2005,求
個棱長為正整數的正方體的體積之和等于2005,求![]() 的最小值,并說明理由;
的最小值,并說明理由;
(2)若![]() 個棱長為正整數的正方體的體積之和等于
個棱長為正整數的正方體的體積之和等于![]() ,求
,求![]() 的最小值,并說明理由.
的最小值,并說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
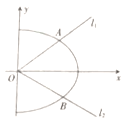
【題目】在直角坐標系![]() 中,橢圓
中,橢圓![]() 的中心在原點,焦點在
的中心在原點,焦點在![]() 軸上,且過點
軸上,且過點![]() ,若
,若![]() 的兩焦點與其中一個頂點能構成一個等邊三角形.
的兩焦點與其中一個頂點能構成一個等邊三角形.
(1)求![]() 的方程.
的方程.
(2)已知過![]() 的兩條直線
的兩條直線![]() ,
,![]() (斜率都存在)與
(斜率都存在)與![]() 的右半部分(
的右半部分(![]() 軸右側)分別相交于
軸右側)分別相交于![]() ,
,![]() 兩點,且
兩點,且![]() 的面積為
的面積為![]() ,試判斷
,試判斷![]() ,
,![]() 的斜率之積是否為定值?若是,求出定值;若不是,說明理由.
的斜率之積是否為定值?若是,求出定值;若不是,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com