Question

已知拋物線y²=4x上兩定點A、B分別在對稱軸兩側，F為焦點，且|AF|=2，|BF|=5，在拋物線的AOB一段上求一點P，使S_△ABP最大，并求面積最大值．

Answer 1

分析：先由題設條件知，|FA|=2，|FB|=5，可根據拋物線的定義求得點A、B的坐標；再由兩點坐標已知，故由兩點間距離公式求出兩點的距離，由直線方程的兩點式求出直線AB的方程；欲求△PAB的面積最大值可轉化為求點P到直線AB的距離的最大值，設出點P的坐標，由點到直線的距離公式建立起點P到直線AB的距離的函數關系式，利用函數的知識求出最值即可．

解答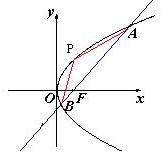：解：不妨設點A在第一象限，B點在第四象限．如圖．
拋物線的焦點F（1，0），點A在第一象限，設A（x₁，y₁），y₁＞0，
由|FA|=2得x₁+1=2，x₁=1，代入y²=4x中得y₁=2，所以A（1，2），…（2分）；
同理B（4，-4），…（4分）
由A（1，2），B（4，-4）得 |AB|=

(1-4)2+(2+4)2

=3

5

…（6分）
直線AB的方程為

y-2

-4-2

=

x-1

4-1

，化簡得2x+y-4=0．…（8分）
再設在拋物線AOB這段曲線上任一點P（x₀，y₀），且0≤x₀≤4，-4≤y₀≤2．
則點P到直線AB的距離d=

|2x0+y0-4|

1+4

=

|2× y0 2 4 +y0-4|

5

=

| 1 2 (y0+1)2- 9 2 |

5

 …（9分）
所以當y₀=-1時，d取最大值

9 5

10

，…（10分）
所以△PAB的面積最大值為S=

1

2

×3

5

×

9 5

10

=

27

4

 …（11分）
此時P點坐標為（

1

4

，-1）．…（12分）．

點評：本小題主要考查拋物線的應用、直線與圓錐曲線的位置關系、兩點間距離公式、點到直線的距離公式、直線方程等基礎知識，考查運算求解能力，考查數形結合思想、化歸與轉化思想．屬于基礎題．