玻璃球盒中裝有各色球12只,其中5紅、4黑、2白、1綠.
(1)從中取1個球,求取得紅或黑的概率;
(2)從中取2個球,求至少一個紅球的概率.
【答案】
分析:(1)利用分類加法計數原理求出“取得紅或黑”包含的基本事件個數,利用古典概型概率公式求出取得紅或黑的概率.
(2)利用分步乘法計數原理和分步加法計數原理求出“至少一個紅球”包含的基本事件個數,利用古典概型概率公式求出概率.
解答:解:(1)從12只球中任取1球得紅球有5種取法,得黑球有4種取法,
得紅球或黑球的共有5+4=9種不同取法,任取一球有12種取法,
所以任取1球得紅球或黑球的概率得
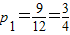
(2)從12只球中任取2球至少一個紅球有2類取法,
得1個紅球有5×7種方法,得兩個紅球有
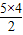
種取法,
從所求概率為
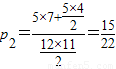 點評:
點評:本題考查利用兩個計數原理求事件的個數、利用古典概型概率公式求事件的概率.

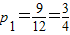
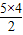 種取法,
種取法,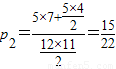


 心算口算巧算一課一練系列答案
心算口算巧算一課一練系列答案