
設函數 .
.
(1)用反證法證明:函數 不可能為偶函數;
不可能為偶函數;
(2)求證:函數 在
在 上單調遞減的充要條件是
上單調遞減的充要條件是 .
.
(1)祥見解析;(2) 祥見解析.
解析試題分析:(1)反證法證明的一般步驟是:先假設結論不正確,從而肯定結論的反面一定成立,在此基礎上結合題目已知條件,經過正確的推理論證得到一個矛盾,從而得到假設不成立,所以結論正確;此題只需假設假設函數 是偶函數,既然是偶函數,則對定義域內的一切x都有
是偶函數,既然是偶函數,則對定義域內的一切x都有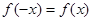 成立,那么我們為了說明假設不成立,即
成立,那么我們為了說明假設不成立,即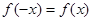 不可能成立,只需任取一個特殊值代入檢驗即可;(2)由于是證明函數
不可能成立,只需任取一個特殊值代入檢驗即可;(2)由于是證明函數 在
在 上單調遞減的充要條件是:
上單調遞減的充要條件是: ;應分充分性和必要性兩個方面來加以證明,先證充分性:
;應分充分性和必要性兩個方面來加以證明,先證充分性: 來證明
來證明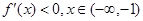 一定成立;再證必要性:由函數
一定成立;再證必要性:由函數 在
在 上單調遞減
上單調遞減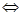
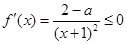 在
在 上恒成立,來證明
上恒成立,來證明 即可,注意已知中的
即可,注意已知中的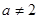 這一條件.
這一條件.
試題解析:(1)假設函數 是偶函數, 2分
是偶函數, 2分
則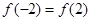 ,即
,即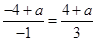 ,解得
,解得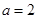 , 4分
, 4分
這與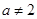 矛盾,所以函數
矛盾,所以函數 不可能是偶函數. 6分
不可能是偶函數. 6分
(2)因為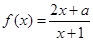 ,所以
,所以 . 8分
. 8分
①充分性:當 時,
時,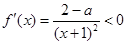 ,
,
所以函數 在
在 單調遞減; 10分
單調遞減; 10分
②必要性:當函數 在
在 單調遞減時,
單調遞減時,
有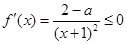 ,即
,即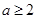 ,又
,又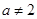 ,所以
,所以 . 13分
. 13分
綜合①②知,原命題成立. 14分
(說明:用函數單調性的定義證明的,類似給分;用反比例函數圖象說理的,適當扣分)
考點:1.反證法;2.函數的單調性;3.充要性的證明.


科目:高中數學 來源: 題型:填空題
某企業投資72萬元興建一座環保建材廠. 第1年各種經營成本為12萬元,以后每年的經營成本增 加4萬元,每年銷售環保建材的收入為50萬元. 則該廠獲取的純利潤達到最大值時是在第 年.
加4萬元,每年銷售環保建材的收入為50萬元. 則該廠獲取的純利潤達到最大值時是在第 年.
查看答案和解析>>
科目:高中數學 來源: 題型:填空題
某地街道呈現東—西、南—北向的網格狀,相鄰街距都為1.兩街道相交的點稱為格點.若以互相垂直的兩條街道為軸建立直角坐標系,現有下述格點 ,
, ,
, ,
, ,
, ,
, 為報刊零售點.請確定一個格點(除零售點外)__________為發行站,使6個零售點沿街道到發行站之間路程的和最短.
為報刊零售點.請確定一個格點(除零售點外)__________為發行站,使6個零售點沿街道到發行站之間路程的和最短.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com