
已知定義在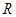 上的函數
上的函數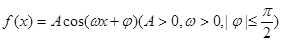 ,最大值與最小值的差為4,相鄰兩個最低點之間距離為
,最大值與最小值的差為4,相鄰兩個最低點之間距離為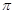 ,函數
,函數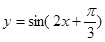 圖象所有對稱中心都在
圖象所有對稱中心都在 圖象的對稱軸上.
圖象的對稱軸上.
(1)求 的表達式;
的表達式;
(2)若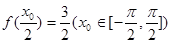 ,求
,求 的值;
的值;
(3)設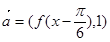 ,
,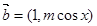 ,
, ,若
,若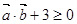 恒成立,求實數
恒成立,求實數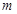 的取值范圍.
的取值范圍.
(1) (2)
(2) (3)
(3)
【解析】(1)由已知中已知定義在R上的函數f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|≤ ),最大值與最小值的差為4,相鄰兩個最低點之間距離為π,我們易計算出A值,及最小正周期,進而求出ω值,再由函數
),最大值與最小值的差為4,相鄰兩個最低點之間距離為π,我們易計算出A值,及最小正周期,進而求出ω值,再由函數 圖象所有的對稱中心都在y=f(x)圖象的對稱軸上,求出φ值,即可得到f(x)的表達式;
圖象所有的對稱中心都在y=f(x)圖象的對稱軸上,求出φ值,即可得到f(x)的表達式;
(2)由 ,結合(1)中所求的函數解析式,可得
,結合(1)中所求的函數解析式,可得 ,
,
進而求出 的值,然后根據兩角差的余弦公式,即可求出答案.
的值,然后根據兩角差的余弦公式,即可求出答案.
(3)由  ,
, 恒成立,可以轉化為函數恒成立問題,構造函數,求出其最值,即可得到答案.
恒成立,可以轉化為函數恒成立問題,構造函數,求出其最值,即可得到答案.
解: (1)依題意可知: ,
,
 與f(x)相差
與f(x)相差 ,即相差
,即相差 ,
,
所以 或
或
 (舍),
(舍),
故 .
……………………4分
.
……………………4分
(2)因為 ,即
,即 ,
,
因為 ,又
,又 ,y=cosx在
,y=cosx在 單調遞增,
單調遞增,
所以 ,所以
,所以 ,
,
于是
 ………9分
………9分
(3)因為 ,
, ,
,
 ,
,
于是 ,得
,得 對于
對于 恒成立,
恒成立,
因為 ,故
,故 . ………………14分
. ………………14分


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源:2013-2014學年天津市薊縣高三上學期期中考試文科數學試卷(解析版) 題型:解答題
已知定義在 上的函數
上的函數 ,其中
,其中 為常數.
為常數.
(1)當 是函數
是函數 的一個極值點,求
的一個極值點,求 的值;
的值;
(2)若函數 在區間
在區間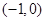 上是增函數,求實數
上是增函數,求實數 的取值范圍;
的取值范圍;
(3)當 時,若
時,若 ,在
,在 處取得最大值,求實數
處取得最大值,求實數 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源:2014屆黑龍江省高二下學期期中考試理科數學試卷(解析版) 題型:解答題
已知定義在 上的函數
上的函數 ,其中
,其中 為常數.
為常數.
(1)若 是函數
是函數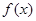 的一個極值點,求
的一個極值點,求 的值;
的值;
(2)若函數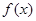 在區間
在區間 上是增函數,求
上是增函數,求 的取值范圍.
的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com