
思路:只要在已知中給出了直徑這一條件,不僅要想到它和半徑的關系,還要想到封閉了它所對的圓周角,便得到了直角三角形,這樣有關直角三角形的性質便可應用了.
探究:如圖2-1-7,以CD為直徑的⊙O交△ACD的兩邊于B、E,連結BE.求證:ADcosA=AB.此題必須先證AD、AB所在的△ABD為直角三角形,此時連結BD,可由直徑所對的圓周角為90°,創造所需的條件.又如圖2-1-8,在⊙O中,直徑AB⊥CD,弦AE⊥CF.要證△ABE≌△CDF,在已知∠A=∠C,AB=CD以后,還缺少一個條件,由AB、CD為直徑,想到連結BE、CF,便可知∠E=∠F=90°,這就為證三角形全等提供了條件.
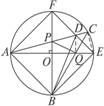
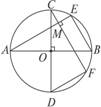
圖2-1-7 圖2-1-8


科目:高中數學 來源: 題型:填空題
 (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分)
(考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分)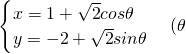 是參數)相切,則b=________.
是參數)相切,則b=________.查看答案和解析>>
科目:高中數學 來源:2012年陜西省寶雞市高三教學質量檢測數學試卷3(文科)(解析版) 題型:解答題
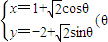 是參數)相切,則b= .
是參數)相切,則b= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com