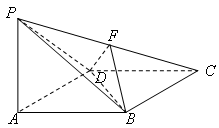
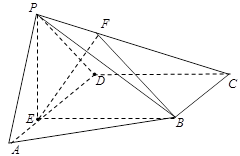
如圖,四棱錐
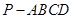
中,
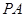
⊥底面
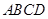
,底面
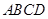
為菱形,點
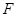
為側(cè)棱
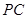
上一點.
(1)若
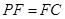
,求證:
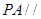
平面

;
(2)若
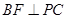
,求證:平面

⊥平面
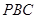
.
試題分析:(1) 要證證
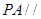
平面

,根據(jù)線面平行的判定定理可轉(zhuǎn)化為線線平行,在本題中可取
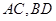
的交點為
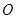
,轉(zhuǎn)化為證明
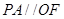
,且
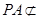
平面

,
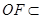
平面

,即可得證
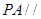
平面

;(2)要證平面

⊥平面
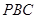
,聯(lián)想到面面垂直的判定定理,可轉(zhuǎn)化為證線面垂直,由于底面
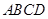
為菱形,則對角線
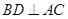
,又
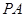
⊥底面
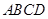
,可得
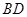
⊥平面
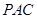
,進而得到
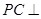
平面

,再加之
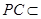
平面
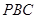
,即可證得平面

⊥平面
.
(1) 證:(1)設(shè)
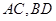
的交點為
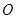
,連
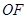
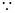
底面
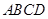
為菱形,
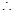
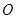
為
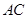
中點,
又
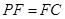
,
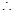
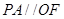
, 5分
且
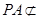
平面

,
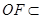
平面

,
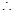
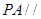
平面

. 7分
(2)
底面
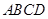
為菱形,
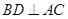
,
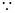
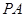
⊥底面
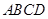
,
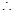
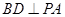
,
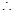
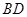
⊥平面
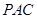
,
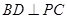
,
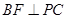
,
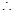
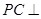
平面

,
又
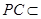
平面
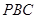
,
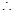
平面

⊥平面
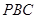
. 14分
練習冊系列答案
相關(guān)習題
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,PDCE為矩形,ABCD為梯形,平面PDCE⊥平面ABCD,∠BAD=∠ADC=90°,AB=AD=

CD=1,PD=

.

(1)若M為PA中點,求證:AC∥平面MDE;
(2)求直線PA與平面PBC所成角的正弦值;
(3)在線段PC上是否存在一點Q(除去端點),使得平面QAD與平面PBC所成銳二面角的大小為

?
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
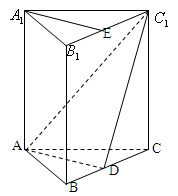
如圖,在正三棱柱
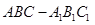
中,點
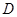
在邊
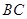
上,
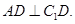
(1)求證:
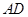
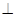
平面
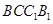
;
(2)如果點

是
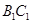
的中點,求證:
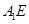
//平面
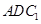
.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
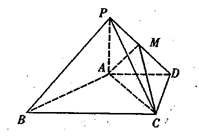
如圖,在四棱錐P-ABCD中,
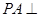
平面ABCD,AD//BC,
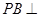
AC,
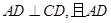
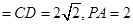
,點M在線段PD上.
(1)求證:
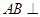
平面PAC;
(2)若二面角M-AC-D的大小為
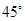
,試確定點M的位置.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,長方體

中,

,

,點
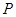
為

的中點。

(1)求證:直線

∥平面

;
(2)求證:平面


平面

;
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,四棱柱ABCD—A
1B
1C
1D
1中,側(cè)棱A
1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA
1=AB=2,E為棱AA
1的中點.

(1)證明B
1C
1⊥CE;
(2)求二面角B
1CEC
1的正弦值;
(3)設(shè)點M在線段C
1E上,且直線AM與平面ADD
1A
1所成角的正弦值為
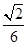
,求線段AM的長.

查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
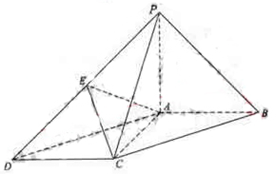
如圖,在底面為平行四邊形的四棱錐
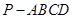
中,
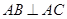
,
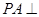
平面
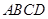
,且
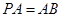
,點
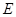
是
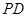
的中點.
(1)求證:
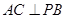
;
(2)求證:
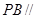
平面
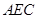
;
(3)求二面角
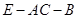
的大小.
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:填空題
[2013·南京模擬]已知l,m是兩條不同的直線,α,β是兩個不同的平面,下列命題:
①若l?α,m?α,l∥β,m∥β,則α∥β;
②若l?α,l∥β,α∩β=m,則l∥m;
③若α∥β,l∥α,則l∥β;
④若l⊥α,m∥l,α∥β,則m⊥β.
其中真命題是________(寫出所有真命題的序號).
查看答案和解析>>
科目:高中數(shù)學
來源:不詳
題型:解答題
如圖,在四棱錐

中,

為

上一點,面

面

,四邊形

為矩形

,

,
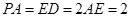
.
(1)已知
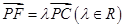
,且

∥面

,求

的值;
(2)求證:

面

,并求點

到面

的距離.
查看答案和解析>>

 中,
中,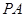 ⊥底面
⊥底面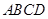 ,底面
,底面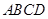 為菱形,點
為菱形,點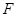 為側(cè)棱
為側(cè)棱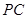 上一點.
上一點.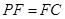 ,求證:
,求證: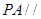 平面
平面 ;
; 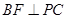 ,求證:平面
,求證:平面 ⊥平面
⊥平面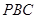 .
.
 期末1卷素質(zhì)教育評估卷系列答案
期末1卷素質(zhì)教育評估卷系列答案 CD=1,PD=
CD=1,PD= .
.
 ?
?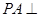 平面ABCD,AD//BC,
平面ABCD,AD//BC,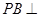 AC,
AC,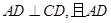
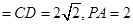 ,點M在線段PD上.
,點M在線段PD上.
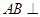 平面PAC;
平面PAC;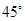 ,試確定點M的位置.
,試確定點M的位置.
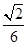 ,求線段AM的長.
,求線段AM的長.