
a>-1

分析:A 把方程化為直角坐標方程,由弦長公式求得圓心到直線的距離d,再由點到直線的距離公式求得tana,從而求得a.
B 由于|x-3|-|x-4|的最小值等于-1,不等式|x-3|-|x-4|<a的解集不是空集,則-1<a.
C 由△PAB∽△PDC,可得
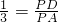
,由PD⊥AD 可得,cos∠APD=
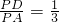
,利用同角三角函數的基本關系求得sin∠APD的值.
解答:A 由題意得 圓C的圓心為(0,6),圓C的方程為 x
2+(y-6)
2=25,
直線
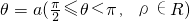
即 y=tana•x,tana•x-y=0.
設圓心到直線的距離等于d,由弦長公式得 8=2

=2
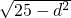
,∴d=3,
再由點到直線的距離公式得 d=3=
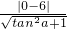
,∴tana=±

.
根據θ范圍知,tana<0,∴tana=-

,a=

,故答案為

.
B 由于|x-3|-|x-4|表示數軸上的x到3的距離減去它到4的距離,最小值等于-1,
如果關于x的不等式|x-3|-|x-4|<a的解集不是空集,則-1<a,即 a>-1,故答案為-1.
C 如圖所示:由題意得∠APB=∠DPC,∠PDC=∠PAB,∠PCD=∠PBA,
∴△PAB∽△PDC,∴

,
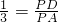
.∵PD⊥AD(直徑對的圓周角等于90°),
∴cos∠APD=
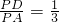
,∴sin∠APD=

,故答案為

.
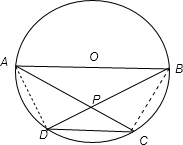
點評:本題考查絕對值不等式的性質,點到直線的距離公式、弦長公式的應用,體現了數形結合的數學思想.

 ),半徑為5,直線
),半徑為5,直線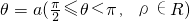 被圓截得的弦長為8,則a=________.
被圓截得的弦長為8,則a=________. a>-1
a>-1 
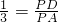 ,由PD⊥AD 可得,cos∠APD=
,由PD⊥AD 可得,cos∠APD=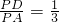 ,利用同角三角函數的基本關系求得sin∠APD的值.
,利用同角三角函數的基本關系求得sin∠APD的值.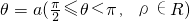 即 y=tana•x,tana•x-y=0.
即 y=tana•x,tana•x-y=0. =2
=2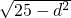 ,∴d=3,
,∴d=3,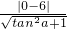 ,∴tana=±
,∴tana=± .
. ,a=
,a= ,故答案為
,故答案為  .
. ,
,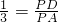 .∵PD⊥AD(直徑對的圓周角等于90°),
.∵PD⊥AD(直徑對的圓周角等于90°),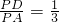 ,∴sin∠APD=
,∴sin∠APD= ,故答案為
,故答案為  .
.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案 (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分)
(考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分) (三選一,考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分)
(三選一,考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評分) (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評閱記分)
(考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評閱記分) (考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評閱記分)
(考生注意:請在下列三題中任選一題作答,如果多做,則按所做的第一題評閱記分)