
【題目】設(shè)![]() 個質(zhì)數(shù)
個質(zhì)數(shù)![]() 構(gòu)成公差為
構(gòu)成公差為![]() 的等差數(shù)列,且
的等差數(shù)列,且![]() .求證
.求證
(1)當(dāng)![]() 是質(zhì)數(shù)時,
是質(zhì)數(shù)時,![]() ;
;
(2)當(dāng)![]() 時,
時,![]() .
.
【答案】(1)見解析(2)見解析
【解析】
(1)因為 ![]() ,
,![]() ,所以,
,所以,![]() 都是大于
都是大于![]() 的質(zhì)數(shù).因此,每一個
的質(zhì)數(shù).因此,每一個![]() 都不能被
都不能被![]() 整除.
整除.
而![]() 被
被![]() 除時只能取
除時只能取![]() 個不同的余數(shù),根據(jù)抽屜原理,至少有兩個數(shù)被
個不同的余數(shù),根據(jù)抽屜原理,至少有兩個數(shù)被![]() 除的余數(shù)相同.設(shè)這兩個數(shù)為
除的余數(shù)相同.設(shè)這兩個數(shù)為![]() 、
、![]() .于是,
.于是,
![]() 能被
能被![]() 整除.
整除.
但![]() ,
,![]() 為質(zhì)數(shù),所以,
為質(zhì)數(shù),所以,![]() .
.
因此,![]() .
.
(2)設(shè)![]() 這15個質(zhì)數(shù)構(gòu)成公差為
這15個質(zhì)數(shù)構(gòu)成公差為![]() 的等差數(shù)列.由于這15個質(zhì)數(shù)必都是奇數(shù),所以,公差
的等差數(shù)列.由于這15個質(zhì)數(shù)必都是奇數(shù),所以,公差![]() 為偶數(shù),即
為偶數(shù),即![]() .
.
由其中的![]() ,
,![]() ,
,![]() 這3個質(zhì)數(shù)成等差數(shù)列,
這3個質(zhì)數(shù)成等差數(shù)列,![]() ,根據(jù)(1)中的結(jié)論,得
,根據(jù)(1)中的結(jié)論,得![]() .
.
由![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 這5個質(zhì)數(shù)成等差數(shù)列,
這5個質(zhì)數(shù)成等差數(shù)列,![]() ,根據(jù)(1)中的結(jié)論,得
,根據(jù)(1)中的結(jié)論,得![]() .
.
由![]() ,
,![]() 和
和![]() 且
且![]() ,可得
,可得![]() .
.
因此,由![]() 知
知![]() .但
.但![]() 為質(zhì)數(shù),所以,
為質(zhì)數(shù),所以,![]() .
.
于是,由![]() 這7個質(zhì)數(shù)成等差數(shù)列,
這7個質(zhì)數(shù)成等差數(shù)列,![]() ,根據(jù)(1)中的結(jié)論,得
,根據(jù)(1)中的結(jié)論,得![]() .
.
同理,由![]() 這11個質(zhì)數(shù)成等差數(shù)列,
這11個質(zhì)數(shù)成等差數(shù)列,![]() , 根據(jù)(1)中的結(jié)論,得
, 根據(jù)(1)中的結(jié)論,得![]() .
.
由![]() 這13個質(zhì)數(shù)成等差數(shù)列,
這13個質(zhì)數(shù)成等差數(shù)列,![]() ,根據(jù)(1)中的結(jié)論,得
,根據(jù)(1)中的結(jié)論,得![]() .
.
因為![]() ,所以,
,所以,![]() ,
,
即![]() .
.
故![]() .
.


 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】在直角坐標(biāo)系xoy中,曲線C1: ![]() (t為參數(shù),t≠0),其中0≤α<π,在以O(shè)為極點,x軸正半軸為極軸的極坐標(biāo)系中,曲線C2:ρ=2sinθ,曲線C3:ρ=2
(t為參數(shù),t≠0),其中0≤α<π,在以O(shè)為極點,x軸正半軸為極軸的極坐標(biāo)系中,曲線C2:ρ=2sinθ,曲線C3:ρ=2 ![]() cosθ.
cosθ.
(1)求C2與C3交點的直角坐標(biāo);
(2)若C2與C1相交于點A,C3與C1相交于點B,求|AB|的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)g(x)=ax2-2ax+1+b(a>0)在區(qū)間[2,4]上的最大值為9,最小值為1,記f(x)=g(|x|)。
(1)求實數(shù)a,b的值;
(2)若不等式f(2k)>1成立,求實數(shù)k的取值范圍;
(3)定義在[p,q]上的函數(shù)![]() (x),設(shè)p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l將區(qū)間[p,q]任意劃分成n個小區(qū)間,如果存在一個常數(shù)M>0,使得和式
(x),設(shè)p=x0<x1<…<xi-1<xi<…<xn=q,x1,x2,…,xn-l將區(qū)間[p,q]任意劃分成n個小區(qū)間,如果存在一個常數(shù)M>0,使得和式![]() 恒成立,則稱函數(shù)
恒成立,則稱函數(shù)![]() (x)為在[p,q]上的有界變差函數(shù)。試判斷函數(shù)f(x)是否為在[0,4]上的有界變差函數(shù)?若是,求M的最小值;若不是,請說明理由。
(x)為在[p,q]上的有界變差函數(shù)。試判斷函數(shù)f(x)是否為在[0,4]上的有界變差函數(shù)?若是,求M的最小值;若不是,請說明理由。
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知橢圓 ![]() 的右焦點為F(2,0),M為橢圓的上頂點,O為坐標(biāo)原點,且△MOF是等腰直角三角形.
的右焦點為F(2,0),M為橢圓的上頂點,O為坐標(biāo)原點,且△MOF是等腰直角三角形.
(1)求橢圓的方程;
(2)過點M分別作直線MA,MB交橢圓于A,B兩點,設(shè)兩直線的斜率分別為k1 , k2 , 且k1+k2=8,證明:直線AB過定點( ![]() ).
).
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,直線AB經(jīng)過⊙O上一點C,⊙O的半徑為3,△AOB是等腰三角形,且C是AB中點,⊙O交直線OB于E、D. 
(1)證明:直線AB與⊙O相切;
(2)若∠CED的正切值為 ![]() ,求OA的長.
,求OA的長.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系![]() 中,直線
中,直線![]() 與拋物線
與拋物線![]() 相交于不同的
相交于不同的![]() 兩點.
兩點.
(1)如果直線![]() 過拋物線的焦點,求
過拋物線的焦點,求![]() 的值;
的值;
(2)如果![]()
![]() ,證明:直線
,證明:直線![]() 必過一定點,并求出該定點.
必過一定點,并求出該定點.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)全集U=R,集合A={x|7﹣6x≤0},集合B={x|y=lg(x+2)},則(UA)∩B等于( )
A.(﹣2, ![]() )
)
B.( ![]() ,+∞)
,+∞)
C.[﹣2, ![]() )
)
D.(﹣2,﹣ ![]() )
)
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在如圖所示的幾何體中,四邊形![]() 為矩形,平面
為矩形,平面![]() ,
, ![]() //
// ![]() ,
,![]() ,
, ![]() ,點
,點![]() 點P在棱
點P在棱![]() 上.
上.
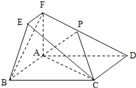
(1)求證: ![]() ;
;
(2)若![]() 是
是![]() 的中點,求異面直線
的中點,求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(3)是否存在正實數(shù)![]() ,使得
,使得![]() ,且滿足二面角
,且滿足二面角![]() 的余弦值為
的余弦值為![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,請說明理由.
的值,若不存在,請說明理由.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某小學(xué)四年級男同學(xué)有45名,女同學(xué)有30名,老師按照分層抽樣的方法組建了一個5人的課外興趣小組.
(Ⅰ)求某同學(xué)被抽到的概率及課外興趣小組中男、女同學(xué)的人數(shù);
(Ⅱ)經(jīng)過一個月的學(xué)習(xí)、討論,這個興趣小組決定選出兩名同學(xué)做某項實驗,方法是先從小組里選出1名同學(xué)做實驗,該同學(xué)做完后,再從小組內(nèi)剩下的同學(xué)中選一名同學(xué)做實驗,求選出的兩名同學(xué)中恰有一名女同學(xué)的概率.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com