【題目】某小學四年級男同學有45名，女同學有30名，老師按照分層抽樣的方法組建了一個5人的課外興趣小組.
（Ⅰ）求某同學被抽到的概率及課外興趣小組中男、女同學的人數；
（Ⅱ）經過一個月的學習、討論，這個興趣小組決定選出兩名同學做某項實驗，方法是先從小組里選出1名同學做實驗，該同學做完后，再從小組內剩下的同學中選一名同學做實驗，求選出的兩名同學中恰有一名女同學的概率.
【答案】(1) 抽到的男同學為3人，女同學為2人;(2) 
.
【解析】
試題分析：（Ⅰ）抽樣的原則是保證每個個體入樣的機會是均等的，分層抽樣的規則是樣本中各部分所占比例與總體中各部分所占比相等，據此可解決此小問；（Ⅱ）運用枚舉法列出所有基本事件，即可解決問題，注意選出的兩名同學是有先后順序的，否則易犯錯，當然枚舉也是講究方法的，否則同樣會發不多就少的錯誤.
試題解析：（Ⅰ）某同學被抽到的概率為
2分
設有
名男同學被抽到，則有
，
抽到的男同學為
人，女同學為
人 4分
（Ⅱ）把3名男同學和2名女同學分別記為
，則選取2名同學的基本事件有
，共
個， 8分
基中恰好有一名女同學有
，有
種 10分
選出的兩名同學中恰有一名女同學的概率為. 12分
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】如圖， 
為正四棱錐
側棱
上異于
， 
的一點，給出下列結論：
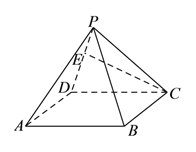
①側面
可以是正三角形．
②側面
可以是直角三角形．
③側面
上存在直線與
平行．
④側面
上存在直線與
垂直．
其中，所有正確結論的序號是__________．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為調查高中生的數學成績與學生自主學習時間之間的相關關系，某重點高中數學教師對新入學的45名學生進行了跟蹤調查，其中每周自主做數學題的時間不少于15小時的有19人，余下的人中，在高三模擬考試中數學平均成績不足120分的占 
，統計成績后，得到如下的2×2列聯表：
分數大于等于120分 | 分數不足120分 | 合計 | |
周做題時間不少于15小時 |
| 4 | 19 |
周做題時間不足15小時 |
|
|
|
合計 |
|
| 45 |
（Ⅰ）請完成上面的2×2列聯表，并判斷能否在犯錯誤的概率不超過0.01的前提下認為“高中生的數學成績與學生自主學習時間有關”；
（Ⅱ）（ i）按照分層抽樣的方法，在上述樣本中，從分數大于等于120分和分數不足120分的兩組學生中抽取9名學生，設抽到的不足120分且周做題時間不足15小時的人數是X，求X的分布列（概率用組合數算式表示）；
（ ii）若將頻率視為概率，從全校大于等于120分的學生中隨機抽取20人，求這些人中周做題時間不少于15小時的人數的期望和方差．
附： 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
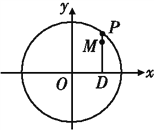
【題目】如圖,設P是圓
上的動點,點D是P在x軸上的投影，M為線段PD上一點,且
，
(1)當P在圓上運動時,求點M的軌跡C的方程；
(2)求過點(3,0)且斜率為
的直線被軌跡C所截線段的長度.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某種產品的廣告費支出
與銷售額
(單位：萬元）具有較強的相關性，且兩者之間有如下對應數據:
| 2 | 4 | 5 | 6 | 8 |
| 28 | 36 | 52 | 56 | 78 |
（1）求關于的線性回歸方程
；
（2）根據（1）中的線性回歸方程，當廣告費支出為10萬元時，預測銷售額是多少？
參考數據： 
，
，
。
附：回歸方程中斜率和截距的最小二乘估計公式分別為：
，
.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
