在△ABC中,已知點A(5,-2)、B(7,3),且邊AC的中點M在y軸上,邊BC的中點N在x軸上.
(1)求點C的坐標;
(2)求直線MN的方程.
【答案】
分析:(1)邊AC的中點M在y軸上,由中點公式得,A,C兩點的橫坐標和的平均數為0,同理,B,C兩點的縱坐標和的平均數為0.構造方程易得C點的坐標.
(2)根據C點的坐標,結合中點公式,我們可求出M,N兩點的坐標,代入兩點式即可求出直線MN的方程.
解答:解:(1)設點C(x,y),
∵邊AC的中點M在y軸上得
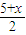
=0,
∵邊BC的中點N在x軸上得
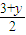
=0,
解得x=-5,y=-3.
故所求點C的坐標是(-5,-3).
(2)點M的坐標是(0,-

),
點N的坐標是(1,0),
直線MN的方程是
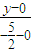
=
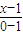
,
即5x-2y-5=0.
點評:在求直線方程時,應先選擇適當的直線方程的形式,并注意各種形式的適用條件,用斜截式及點斜式時,直線的斜率必須存在,而兩點式不能表示與坐標軸垂直的直線,截距式不能表示與坐標軸垂直或經過原點的直線,故在解題時,若采用截距式,應注意分類討論,判斷截距是否為零;若采用點斜式,應先考慮斜率不存在的情況.

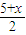 =0,
=0,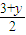 =0,
=0, ),
),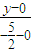 =
=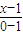 ,
,

 初中學業考試導與練系列答案
初中學業考試導與練系列答案