
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 與x軸交于A,B兩點,點Q的坐標為
與x軸交于A,B兩點,點Q的坐標為![]() .
.
(1)是否存在b,使得![]() ,如果存在求出b值;如果不存在,說明理由;
,如果存在求出b值;如果不存在,說明理由;
(2)過A,B,Q三點的圓面積最小時,求圓的方程.
科目:高中數學 來源: 題型:
【題目】據氣象局統計,某市2019年從1月1日至1月30日這30天里有26天出現霧霾天氣.國際上通常用環境空氣質量指數(AQI)來描述污染狀況,下表是某氣象觀測點記錄的連續4天里,該市AQI指數![]() 與當天的空氣水平可見度
與當天的空氣水平可見度![]() 的情況.
的情況.
AQI指數 | 900 | 700 | 300 | 100 |
空氣水平可見度 | 0.5 | 3.5 | 6.5 | 9.5 |
(1)設![]() ,根據表中的數據,求出
,根據表中的數據,求出![]() 關于
關于![]() 的回歸方程;
的回歸方程;
(2)若某天該市AQT指數![]() ,那么當天空氣水平可見度大約為多少?
,那么當天空氣水平可見度大約為多少?
附:參考數據:![]() ,
,![]() .
.
參考公式:線性回歸力程![]() 中,
中,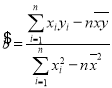 ,
,![]() ,其中
,其中![]() 為樣本平均數.
為樣本平均數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}是等差數列,Sn為{an}的前n項和,且a10=19,S10=100;數列{bn}對任意n∈N*,總有b1![]() b2
b2![]() b3…bn﹣1
b3…bn﹣1![]() bn=an+2成立.
bn=an+2成立.
(1)求數列{an}和{bn}的通項公式;
(2)記cn=(﹣1)n![]() ,求數列{cn}的前n項和Tn.
,求數列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=![]() x3
x3![]() (a2+a+2)x2+a2(a+2)x,a∈R.
(a2+a+2)x2+a2(a+2)x,a∈R.
(1)當a=![]() 1時,求函數y=f(x)的單調區間;
1時,求函數y=f(x)的單調區間;
(2)求函數y=f(x)的極值點.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《九章算術》將底面為長方形且有一條側棱與底面垂直的四棱錐稱之為陽馬,將四個面都為直角三角形的四面體稱之為鱉臑.下圖所示的陽馬![]() 中,側棱
中,側棱![]() 底面ABCD,且
底面ABCD,且![]() ,則當點E在下列四個位置:PA中點、PB中點、PC中點、PD中點時分別形成的四面體
,則當點E在下列四個位置:PA中點、PB中點、PC中點、PD中點時分別形成的四面體![]() 中,鱉臑有( )個.
中,鱉臑有( )個.
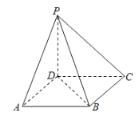
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設拋物線![]() 的焦點為F,準線為l,A為C上一點,已知以F為圓心,FA為半徑的圓F交l于M.N點.
的焦點為F,準線為l,A為C上一點,已知以F為圓心,FA為半徑的圓F交l于M.N點.
(1)若![]() ,
,![]() 的面積為
的面積為![]() ,求拋物線方程;
,求拋物線方程;
(2)若A.M.F三點在同一直線m上,直線n與m平行,且n與C只有一個公共點,求坐標原點到直線n、m距離的比值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() .
.
(1)若函數![]() 在區間
在區間![]() (
(![]() 為自然對數的底數)上有唯一的零點,求實數
為自然對數的底數)上有唯一的零點,求實數![]() 的取值范圍;
的取值范圍;
(2)若在![]() (
(![]() 為自然對數的底數)上存在一點
為自然對數的底數)上存在一點![]() ,使得
,使得![]() 成立,求實數
成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(1)若關于![]() 的方程
的方程![]() 在
在![]() 上恰有兩個不相等的實數根,求實數
上恰有兩個不相等的實數根,求實數![]() 的取值范圍;
的取值范圍;
(2)是否存在實數![]() 使得
使得![]() 總成立?若存在,求實數
總成立?若存在,求實數![]() 的值;若不存在,說明理由.
的值;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com