
【題目】已知函數f(x)=xe2x﹣lnx﹣ax.
(1)當a=0時,求函數f(x)在[ ![]() ,1]上的最小值;
,1]上的最小值;
(2)若x>0,不等式f(x)≥1恒成立,求a的取值范圍;
(3)若x>0,不等式f( ![]() )﹣1≥
)﹣1≥ ![]() e
e ![]() +
+ ![]() 恒成立,求a的取值范圍.
恒成立,求a的取值范圍.
【答案】
(1)解:a=0時,f(x)=xe2x﹣lnx,
∴ ![]() ,
, ![]() ,
,
∴函數f′(x)在(0,+∞)上是增函數,
又函數f′(x)的值域為R,
故x0>0,使得f′(x0)=(2x0+1)e ![]() ﹣
﹣ ![]() =0,
=0,
又∵ ![]() ,∴
,∴ ![]() ,所以當x∈[
,所以當x∈[ ![]() ]時,f′(x)>0,
]時,f′(x)>0,
即函數f(x)在區間[ ![]() ,1]上遞增,所以
,1]上遞增,所以 ![]()
(2)解: ![]() ,
,
由(1)知函數f′(x)在(0,+∞)上是增函數,且x0>0,使得f′(x0)=0,
進而函數f(x)在區間(0,x0)上遞減,在(x0,+∞)上遞增,
![]() ﹣lnx0﹣ax0,
﹣lnx0﹣ax0,
由f′(x0)=0,得:(2x0+1)e ![]() ﹣
﹣ ![]() ﹣a=0,
﹣a=0,
∴ ![]() ,∴f(x0)=1﹣lnx0﹣2x02
,∴f(x0)=1﹣lnx0﹣2x02 ![]() ,
,
∵x>0,不等式f(x)≥1恒成立,
∴1﹣lnx0﹣2x02e ![]() ≥1,∴lnx0+2x02
≥1,∴lnx0+2x02 ![]() ≤0,
≤0,
∴ ![]() ≤2+0=2.
≤2+0=2.
∴a的取值范圍是(﹣∞,2]
(3)解:由f( ![]() )﹣1≥
)﹣1≥ 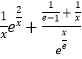 ,
,
得 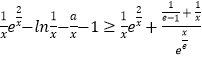 ,
,
∴xlnx﹣x﹣a≥ ![]() ,∴a
,∴a  對任意x>0成立,
對任意x>0成立,
令函數g(x)=xlnx﹣x﹣ ![]() ,∴
,∴ ![]() ,
,
當x>1時,g′(x)>0,當0<x<1時,g′(x)<0,
∴當x=1時,函數g(x)取得最小值g(1)=﹣1﹣ ![]() =﹣1﹣
=﹣1﹣ ![]() ,
,
∴a≤﹣1﹣ ![]() .
.
∴a的取值范圍是(﹣∞,﹣1﹣ ![]() )
)
【解析】(1.)a=0時, ![]() ,
, ![]() ,由此利用導數性質能求出函數f(x)在[
,由此利用導數性質能求出函數f(x)在[ ![]() ,1]上的最小值. (2.)
,1]上的最小值. (2.) ![]() ,函數f(x)在區間(0,x0)上遞減,在(x0 , +∞)上遞增,由x>0,不等式f(x)≥1恒成立,得lnx0+2x02
,函數f(x)在區間(0,x0)上遞減,在(x0 , +∞)上遞增,由x>0,不等式f(x)≥1恒成立,得lnx0+2x02 ![]() ≤0,由此能求出a的取值范圍.(3)由f(
≤0,由此能求出a的取值范圍.(3)由f( ![]() )﹣1≥
)﹣1≥ 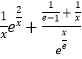 ,得a
,得a  對任意x>0成立,令函數g(x)=xlnx﹣x﹣
對任意x>0成立,令函數g(x)=xlnx﹣x﹣ ![]() ,則
,則 ![]() ,由此利用導數性質能求出a的取值范圍.
,由此利用導數性質能求出a的取值范圍.


科目:高中數學 來源: 題型:
【題目】設函數 ![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
①f(x)的圖象關于直線 ![]() 對稱
對稱
②f(x)的圖象關于點 ![]() 對稱
對稱
③f(x)的圖象向左平移 ![]() 個單位,得到一個偶函數的圖象
個單位,得到一個偶函數的圖象
④f(x)的最小正周期為π,且在 ![]() 上為增函數.
上為增函數.
A.③
B.①③
C.②④
D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=|x+m|+|2x﹣1|(m∈R) (I)當m=﹣1時,求不等式f(x)≤2的解集;
(II)設關于x的不等式f(x)≤|2x+1|的解集為A,且[ ![]() ,2]A,求實數m的取值范圍.
,2]A,求實數m的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知Sn是等比數列{an}的前n項和,S3 , S9 , S6成等差數列. (Ⅰ)求證:a2 , a8 , a5成等差數列;
(Ⅱ)若等差數列{bn}滿足b1=a2=1,b3=a5 , 求數列{an3bn}的前n項和Tn .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給出以下四個結論: ①函數 ![]() 的對稱中心是(﹣1,2);
的對稱中心是(﹣1,2);
②若關于x的方程 ![]() 沒有實數根,則k的取值范圍是k≥2;
沒有實數根,則k的取值范圍是k≥2;
③在△ABC中,“bcosA=acosB”是“△ABC為等邊三角形”的充分不必要條件;
④若 ![]() 的圖象向右平移φ(φ>0)個單位后為奇函數,則φ最小值是
的圖象向右平移φ(φ>0)個單位后為奇函數,則φ最小值是 ![]() .
.
其中正確的結論是 .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】知函數f(x)=ax2﹣2x+lnx(a≠0,a∈R).
(1)判斷函數 f (x)的單調性;
(2)若函數 f (x)有兩個極值點x1 , x2 , 求證:f(x1)+f(x2)<﹣3.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com