【題目】已知定點
，橫坐標不小于
的動點在
軸上的射影為
，若
.
（1）求動點
的軌跡
的方程；
（2）若點
不在直
線上，并且直線
與曲線相交于
兩個不同點.問是否存在常數
使得當
的值變化時，直線
斜率之和是一個定值.若存在，求出的值；若不存在，請說明理由.
閱讀快車系列答案科目：高中數學 來源： 題型：
【題目】已知圓O；x2+y2=4，F1（-1，0），F2（1，0），點D圓O上一動點，2
=
，點C在直線EF1上，且
=0，記點C的軌跡為曲線W．
（1）求曲線W的方程；
（2）已知N（4，0），過點N作直線l與曲線W交于A，B不同兩點，線段AB的中垂線為l'，線段AB的中點為Q點，記P與y軸的交點為M，求|MQ|的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知動圓
過定點
，且和直線
相切，動圓圓心形成的軌跡是曲線
，過點
的直線與曲線交于
兩個不同的點.
（1）求曲線的方程；
（2）在曲線上是否存在定點
，使得以
為直徑的圓恒過點？若存在，求出點坐標；若不存在，說明理由.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某小區為了調查居民的生活水平，隨機從小區住戶中抽取
個家庭，得到數據如下：
家庭編號 | 1 | 2 | 3 | 4 | 5 | 6 |
月收入x（千元） | 20 | 30 | 35 | 40 | 48 | 55 |
月支出y（千元） | 4 | 5 | 6 | 8 | 8 | 11 |
參考公式：回歸直線的方程是：
，其中，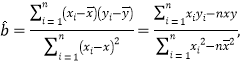
.
（1）據題中數據，求月支出
（千元）關于月收入
（千元）的線性回歸方程（保留一位小數）；
（2）從這個家庭中隨機抽取
個，求月支出都少于
萬元的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】為響應黨中央號召，學校以“我們都是追夢人”為主題舉行知識競賽。現有10道題，其中6道甲類題，4道乙類題，王同學從中任取3道題解答.
（Ⅰ）求王同學至少取到2道乙類題的概率;
（Ⅱ）如果王同學答對每道甲類題的概率都是
，答對每道乙類題的概率都是
，且各題答對與否相互獨立，已知王同學恰好選中2道甲類題，1道乙類題，用
表示王同學答對題的個數，求隨機變量的分布列和數學期望.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖（1），在直角梯形
中，
為
的中點，四邊形
為正方形，將
沿
折起，使點
到達點
，如圖（2），
為
的中點，且
，點
為線段
上的一點.
（1）證明：
；
（2）當
與
夾角最小時，求平面
與平面
所成銳二面角的余弦值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
