Question

設函數(shù)f（x）=a|x|+（a，b為常數(shù)），且①f（-2）=0；②f（x）有兩個單調(diào)遞增區(qū)間，則同時滿足上述條件的一個有序數(shù)對（a，b）為    ．

Answer 1

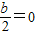【答案】分析：由f（-2）=2a-可得b=4a，從而可得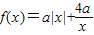=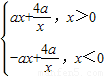，由函數(shù)的定義域為（-∞，0）（0，+∞），當a＞0時，函數(shù)在（2，+∞）單調(diào)遞增，在（-∞，0），（0，2）單調(diào)遞減，當a＜0時，函數(shù)在（0，+∞）在（0，2）單調(diào)遞增，在（-∞，0）單調(diào)遞減，當a=0時，函數(shù)f（x）=0不具有單調(diào)性，從而可得
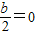解答：解：由f（-2）=2a-可得，b=4a
∴=
∴函數(shù)的定義域為（-∞，0）（0，+∞）
∵f（x）有兩個單調(diào)遞增區(qū)間
當a＞0時，函數(shù)在（2，+∞）單調(diào)遞增，在（-∞，0），（0，2）單調(diào)遞減，不符合題意
當a＜0時，函數(shù)在（0，+∞）在（0，2）單調(diào)遞增，在（-∞，0）單調(diào)遞減
當a=0時，函數(shù)f（x）=0不具有單調(diào)性
故滿足條件的a＜0
故答案為：（t，4t）（t＜0）
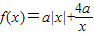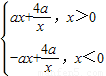
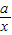點評：本題主要考查了形如f（x）=ax+的單調(diào)性與參數(shù)a的取值范圍的關系，解題的關鍵是要靈活利用基本初等函數(shù)的單調(diào)行．