Question

求直線y=2x+3與拋物線y=x²所圍成的圖形的面積S=    ．

Answer 1

【答案】分析：本題考查的知識點是定積分的幾何意義，首先我們要聯立兩個曲線的方程，判斷他們的交點，以確定積分公式中x的取值范圍，再根據定積分的幾何意義，所求圖形的面積為S=∫_-1³（2x+3）dx-∫_-1³x²dx，計算后即得答案．
解答：解：由方程組
解得，x₁=-1，x₂=3．
故所求圖形的面積為S=∫_-1³（2x+3）dx-∫_-1³x²dx
=20-=
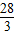
故答案為：
點評：在直角坐標系下平面圖形的面積的四個步驟：1．作圖象；2．求交點；3．用定積分表示所求的面積；4．微積分基本定理求定積分．