
【題目】已知定義域為![]() 的函數
的函數![]() 是奇函數.
是奇函數.
(1) 求實數![]() 的值;
的值;
(2) 判斷并用定義證明該函數在定義域![]() 上的單調性;
上的單調性;
(3) 若方程![]() 在
在![]() 內有解,求實數
內有解,求實數![]() 的取值范圍.
的取值范圍.
科目:高中數學 來源: 題型:
【題目】定義區間![]() 的長度
的長度![]() 均為
均為![]() ,多個互無交集的區間的并集長度為各區間長度之和,例如
,多個互無交集的區間的并集長度為各區間長度之和,例如![]() 的長度
的長度![]() 。用
。用![]() 表示不超過
表示不超過![]() 的最大整數,例如
的最大整數,例如![]() 。記
。記![]() 。設
。設![]() ,
,![]() ,若用
,若用![]() 、
、![]() 和
和![]() 分別表示不等式
分別表示不等式![]() 、方程
、方程![]() 和不等式
和不等式![]() 解集區間的長度,則當
解集區間的長度,則當![]() 時,
時,![]() ____________.
____________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】橢圓E: ![]() +
+ ![]() =1(a>b>0)的焦點到直線x﹣3y=0的距離為
=1(a>b>0)的焦點到直線x﹣3y=0的距離為 ![]() ,離心率為
,離心率為 ![]() ,拋物線G:y2=2px(p>0)的焦點與橢圓E的焦點重合;斜率為k的直線l過G的焦點與E交于A,B,與G交于C,D.
,拋物線G:y2=2px(p>0)的焦點與橢圓E的焦點重合;斜率為k的直線l過G的焦點與E交于A,B,與G交于C,D.
(1)求橢圓E及拋物線G的方程;
(2)是否存在學常數λ,使 ![]() 為常數,若存在,求λ的值,若不存在,說明理由.
為常數,若存在,求λ的值,若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
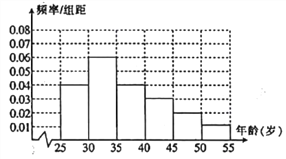
【題目】某高校進行社會實踐,對![]() 歲的人群隨機抽取 1000 人進行了一次是否開通“微博”的調查,開通“微博”的為“時尚族”,否則稱為“非時尚族”.通過調查得到到各年齡段人數的頻率分布直方圖如圖所示,其中在
歲的人群隨機抽取 1000 人進行了一次是否開通“微博”的調查,開通“微博”的為“時尚族”,否則稱為“非時尚族”.通過調查得到到各年齡段人數的頻率分布直方圖如圖所示,其中在![]() 歲,
歲, ![]() 歲年齡段人數中,“時尚族”人數分別占本組人數的
歲年齡段人數中,“時尚族”人數分別占本組人數的![]() 、
、![]() .
.
(1)求![]() 歲與
歲與![]() 歲年齡段“時尚族”的人數;
歲年齡段“時尚族”的人數;
(2)從![]() 歲和
歲和![]() 歲年齡段的“時尚族”中,采用分層抽樣法抽取6人參加網絡時尚達人大賽,其中兩人作為領隊.求領隊的兩人年齡都在
歲年齡段的“時尚族”中,采用分層抽樣法抽取6人參加網絡時尚達人大賽,其中兩人作為領隊.求領隊的兩人年齡都在![]() 歲內的概率。
歲內的概率。
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設O是坐標原點,橢圓C:x2+3y2=6的左右焦點分別為F1 , F2 , 且P,Q是橢圓C上不同的兩點,
(1)若直線PQ過橢圓C的右焦點F2 , 且傾斜角為30°,求證:|F1P|、|PQ|、|QF1|成等差數列;
(2)若P,Q兩點使得直線OP,PQ,QO的斜率均存在.且成等比數列.求直線PQ的斜率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓![]() 的左、右焦點為
的左、右焦點為![]() ,右頂點為
,右頂點為![]() ,上頂點為
,上頂點為![]() ,若
,若![]() ,
, ![]() 與
與![]() 軸垂直,且
軸垂直,且![]() .
.
(1)求橢圓方程;
(2)過點![]() 且不垂直于坐標軸的直線與橢圓交于
且不垂直于坐標軸的直線與橢圓交于![]() 兩點,已知點
兩點,已知點![]() ,當
,當![]() 時,求滿足
時,求滿足![]() 的直線
的直線![]() 的斜率
的斜率![]() 的取值范圍.
的取值范圍.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了研究鐘表與三角函數的關系,以9點與3點所在直線為x軸,以6點與12點為y軸,設秒針針尖指向位置P(x,y),若初始位置為P0( ![]() ,
, ![]() ),秒針從P0(注此時t=0)開始沿順時針方向走動,則點P的縱坐標y與時間t(秒)的函數關系為( )
),秒針從P0(注此時t=0)開始沿順時針方向走動,則點P的縱坐標y與時間t(秒)的函數關系為( )
A.y=sin( ![]() t+
t+ ![]() )
)
B.y=sin( ![]() t﹣
t﹣ ![]() )
)
C.y=sin(﹣ ![]() t+
t+ ![]() )
)
D.y=sin(﹣ ![]() t﹣
t﹣ ![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方形ABCD邊長為2,以D為圓心、DA為半徑的圓弧與以BC為直徑的半圓O交于點F,連結CF并延長交AB于點E. 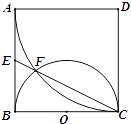
(1)求證:AE=EB;
(2)求EFFC的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com