
【題目】某校高三共有800名學生,為了解學生3月月考生物測試情況,根據男女學生人數差異較大,從中隨機抽取了200名學生,記錄他們的分數,并整理得如圖頻率分布直方圖.
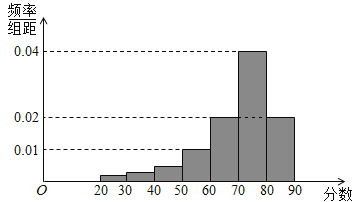
(1)若成績不低于60分的為及格,成績不低于80分的為優秀,試估計總體中合格的有多少人?優秀的有多少人?
(2)已知樣本中有一半的女生分數不小于80,且樣本中不低于80分的男女生人數之比2:3,試估計總體中男生和女生人數的比例.
【答案】(1)及格的有640人,優秀的有160人.(2)![]()
【解析】試題分析:(1)根據頻率分布直方圖得到成績及格和成績優秀的頻率,根據“頻數=頻率×樣本容量”得的人數;(2)根據頻率分布直方圖得到樣本中不低于80分的女生人數為40人,所以樣本中分數不小于80的女生人數為![]() ,從而得到樣本中的女生人數為
,從而得到樣本中的女生人數為![]() ,男生人數為
,男生人數為![]() ,然后根據分層抽樣的原理可得男生和女生人數的估計比例。
,然后根據分層抽樣的原理可得男生和女生人數的估計比例。
試題解析:
(1)根據頻率分布直方圖可知,
總體中及格的人數估計為![]() ,
,
總體中優秀的人數估計為![]() ,
,
所以估計總體中及格的有640人,優秀的有160人.
(2)由題意可知,樣本中分數不小于80的學生人數為![]() ,
,
所以樣本中分數不小于80的女生人數為![]() ,
,
所以樣本中的女生人數為![]() ,男生人數為
,男生人數為![]() ,
,
男生和女生人數的比例為![]() ,
,
所以根據分層抽樣原理,總體中男生和女生人數的比例估計為![]() .
.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】某港口船舶停靠的方案是先到先停.
(1)若甲乙兩艘船同時到達港口,雙方約定各派一名代表猜拳:從1,2,3,4,5中各隨機選一個數,若兩數之和為偶數,則甲先停靠;若兩數之和為奇數,則乙先停靠,這種規則是否公平?請說明理由.
(2)根據以往經驗,甲船將于早上![]() 到達,乙船將于早上
到達,乙船將于早上![]() 到達,請應用隨機模擬的方法求甲船先停靠的概率,隨機數模擬實驗數據參考如下:記
到達,請應用隨機模擬的方法求甲船先停靠的概率,隨機數模擬實驗數據參考如下:記![]() ,
, ![]() 都是
都是![]() 之間的均勻隨機數,用計算機做了100次試驗,得到的結果有12次滿足
之間的均勻隨機數,用計算機做了100次試驗,得到的結果有12次滿足![]() ,有6次滿足
,有6次滿足![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓![]() 的圓心在直線
的圓心在直線![]() :
: ![]() 上,與直線
上,與直線![]() :
: ![]() 相切,且截直線
相切,且截直線![]() :
: ![]() 所得弦長為6
所得弦長為6
(Ⅰ)求圓![]() 的方程
的方程
(Ⅱ)過點![]() 是否存在直線
是否存在直線![]() ,使以
,使以![]() 被圓
被圓![]() 截得弦
截得弦![]() 為直徑的圓經過原點?若存在,寫出直線的方程;若不存在,說明理由.
為直徑的圓經過原點?若存在,寫出直線的方程;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(I)求函數![]() 的對稱軸方程;
的對稱軸方程;
(II)將函數![]() 的圖象上各點的縱坐標保持不變,橫坐標伸長為原來的2倍,然后再向左平移
的圖象上各點的縱坐標保持不變,橫坐標伸長為原來的2倍,然后再向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象.若
的圖象.若![]() 分別是△ABC三個內角A,B,C的對邊,a=2,c=4,且
分別是△ABC三個內角A,B,C的對邊,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() .
.
(I)求函數![]() 的對稱軸方程;
的對稱軸方程;
(II)將函數![]() 的圖象上各點的縱坐標保持不變,橫坐標伸長為原來的2倍,然后再向左平移
的圖象上各點的縱坐標保持不變,橫坐標伸長為原來的2倍,然后再向左平移![]() 個單位,得到函數
個單位,得到函數![]() 的圖象.若
的圖象.若![]() 分別是△ABC三個內角A,B,C的對邊,a=2,c=4,且
分別是△ABC三個內角A,B,C的對邊,a=2,c=4,且![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數f(x)的解析式滿足 ![]() .
.
(1)求函數f(x)的解析式;
(2)當a=1時,試判斷函數f(x)在區間(0,+∞)上的單調性,并加以證明;
(3)當a=1時,記函數 ![]() ,求函數g(x)在區間
,求函數g(x)在區間 ![]() 上的值域.
上的值域.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】分層抽樣是將總體分成互不交叉的層,然后按照一定的比例,從各層獨立地抽取一定數量的個體,組成一個樣本的抽樣方法;在《九章算術》第三章“衰分”中有如下問題:“今有甲持錢五百六十,乙持錢三百五十,丙持錢一百八十,凡三人俱出關,關稅百錢.欲以錢多少衰出之,問各幾何?”其譯文為:今有甲持560錢,乙持350錢,丙持180錢,甲、乙、丙三人一起出關,關稅共100錢,要按照各人帶錢多少的比例進行交稅,問三人各應付多少稅?則下列說法錯誤的是( )
A. 甲應付![]() 錢 B. 乙應付
錢 B. 乙應付![]() 錢
錢
C. 丙應付![]() 錢 D. 三者中甲付的錢最多,丙付的錢最少
錢 D. 三者中甲付的錢最多,丙付的錢最少
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點的動直線![]() 與圓
與圓![]() 相交于不同的兩點
相交于不同的兩點![]() .
.
(1)求線段![]() 的中點
的中點![]() 的軌跡
的軌跡![]() 的方程;
的方程;
(2)是否存在實數![]() ,使得直線
,使得直線![]() 與曲線
與曲線![]() 只有一個交點?若存在,求出
只有一個交點?若存在,求出![]() 的取值范圍;若不存在,請說明理由.
的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學為調研學生在![]() ,
, ![]() 兩家餐廳用餐的滿意度,從在
兩家餐廳用餐的滿意度,從在![]() ,
, ![]() 兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
兩家餐廳都用過餐的學生中隨機抽取了100人,每人分別對這兩家餐廳進行評分,滿分均為60分.
整理評分數據,將分數以10為組距分成6組: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,得到
,得到![]() 餐廳分數的頻率分布直方圖,和
餐廳分數的頻率分布直方圖,和![]() 餐廳分數的頻數分布表:
餐廳分數的頻數分布表:
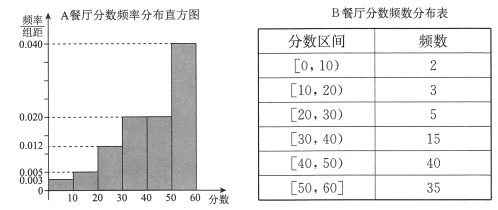
(Ⅰ)在抽樣的100人中,求對![]() 餐廳評分低于30的人數;
餐廳評分低于30的人數;
(Ⅱ)從對![]() 餐廳評分在
餐廳評分在![]() 范圍內的人中隨機選出2人,求2人中恰有1人評分在
范圍內的人中隨機選出2人,求2人中恰有1人評分在![]() 范圍內的概率;
范圍內的概率;
(Ⅲ)如果從![]() ,
, ![]() 兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
兩家餐廳中選擇一家用餐,你會選擇哪一家?說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com