
【題目】已知函數![]() .
.
(1)設![]() .
.
①若![]() ,曲線
,曲線![]() 在
在![]() 處的切線過點
處的切線過點![]() ,求
,求![]() 的值;
的值;
②若![]() ,求
,求![]() 在區間
在區間![]() 上的最大值.
上的最大值.
(2)設![]() 在
在![]() ,
, ![]() 兩處取得極值,求證:
兩處取得極值,求證: ![]() ,
, ![]() 不同時成立.
不同時成立.
【答案】(1)①![]() 或
或![]() .②
.②![]() 的最大值為0.(2)見解析.
的最大值為0.(2)見解析.
【解析】(1)根據題意,在①中,利用導數的幾何意義求出切線方程,再將點![]() 代入即求出
代入即求出![]() 的值,在②中,通過函數的導數來研究其單調性,并求出其極值,再比較端點值,從而求出最大值;(2)由題意可采用反證法進行證明,假設問題成立,再利用函數的導數來判斷函數的單調性,證明其結果與假設產生矛盾,從而問題可得證.
的值,在②中,通過函數的導數來研究其單調性,并求出其極值,再比較端點值,從而求出最大值;(2)由題意可采用反證法進行證明,假設問題成立,再利用函數的導數來判斷函數的單調性,證明其結果與假設產生矛盾,從而問題可得證.
試題解析:(1)當![]() 時,
時, ![]() .
.
①若![]() ,則
,則![]() ,
,
從而![]() ,
,
故曲線![]() 在
在![]() 處的切線方程為
處的切線方程為![]()
![]() .
.
將點![]() 代入上式并整理得
代入上式并整理得![]()
![]() ,
,
解得![]() 或
或![]() .
.
②若![]() ,則令
,則令![]() ,解得
,解得![]() 或
或![]() .
.
(ⅰ)若![]() ,則當
,則當![]() 時,
時, ![]() ,
,
所以![]() 為區間
為區間![]() 上的增函數,
上的增函數,
從而![]() 的最大值為
的最大值為![]() .
.
(ii)若![]() ,列表:
,列表:

所以![]() 的最大值為
的最大值為![]() .
.
綜上, ![]() 的最大值為0.
的最大值為0.
(2)假設存在實數![]() ,使得
,使得![]() 與
與![]() 同時成立.
同時成立.
不妨設![]() ,則
,則![]() .
.
因為![]() ,
, ![]() 為
為![]() 的兩個極值點,
的兩個極值點,
所以![]()
![]() .
.
因為![]() ,所以當
,所以當![]() 時,
時, ![]() ,
,
故![]() 為區間
為區間![]() 上的減函數,
上的減函數,
從而![]() ,這與
,這與![]() 矛盾,
矛盾,
故假設不成立.
既不存在實數![]() ,
, ![]() ,
, ![]() ,使得
,使得![]() ,
, ![]() 同時成立.
同時成立.


科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,已知曲線
中,已知曲線![]() 的方程為
的方程為![]() (
(![]() 為參數),以坐標原點
為參數),以坐標原點![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程為
的極坐標方程為![]() (
(![]() ).
).
(1)求曲線![]() 的普通方程和曲線
的普通方程和曲線![]() 的直角坐標方程;
的直角坐標方程;
(2)曲線![]() 上有3個點到曲線
上有3個點到曲線![]() 的距離等于1,求
的距離等于1,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為調查某地區老人是否需要志愿者提供幫助,用簡單隨機抽樣方法從該地區調查了500位老年人,結果如下:
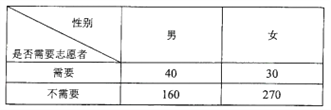
(Ⅰ)估計該地區老年人中,需要志愿者提供幫助的老年人的比例;
(Ⅱ)能否有![]() 的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
的把握認為該地區的老年人是否需要志愿者提供幫助與性別有關?
(Ⅲ)根據(Ⅱ)的結論,能否提供更好的調查方法來估計該地區的老年人中,需要志愿者提供幫助的老年人的比例?說明理由.
附: 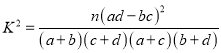
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在某次水下科研考察活動中,需要潛水員潛入水深為60米的水底進行作業,根據已往經驗,潛水員下潛的平均速度為![]() (米/單位時間),每單位時間的用氧量為
(米/單位時間),每單位時間的用氧量為![]() (升),在水底作業10個單位時間,每單位時間用氧量為
(升),在水底作業10個單位時間,每單位時間用氧量為![]() (升),返回水面的平均速度為
(升),返回水面的平均速度為![]() (米/單位時間),每單位時間用氧量為
(米/單位時間),每單位時間用氧量為![]() (升),記該潛水員在此次考察活動中的總用氧量為
(升),記該潛水員在此次考察活動中的總用氧量為![]() (升).
(升).
(1)求![]() 關于
關于![]() 的函數關系式;
的函數關系式;
(2)若![]() ,求當下潛速度
,求當下潛速度![]() 取什么值時,總用氧量最少.
取什么值時,總用氧量最少.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知城![]() 和城
和城![]() 相距
相距![]() ,現計劃以
,現計劃以![]() 為直徑的半圓上選擇一點
為直徑的半圓上選擇一點![]() (不與點
(不與點![]() ,
, ![]() 重合)建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關,對城
重合)建造垃圾處理廠.垃圾處理廠對城市的影響度與所選地點到城市的距離有關,對城![]() 和城
和城![]() 的總影響度為對城
的總影響度為對城![]() 與城
與城![]() 的影響度之和.記點到
的影響度之和.記點到![]() 城
城![]() 的距離為
的距離為![]() ,建在
,建在![]() 處的垃圾處理廠對城
處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度為
的總影響度為![]() .統計調查表明:垃圾處理廠對城
.統計調查表明:垃圾處理廠對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比例關系,比例系數為4;對城
的距離的平方成反比例關系,比例系數為4;對城![]() 的影響度與所選地點到城
的影響度與所選地點到城![]() 的距離的平方成反比例關系,比例系數為
的距離的平方成反比例關系,比例系數為![]() .當垃圾處理廠建在
.當垃圾處理廠建在![]() 的中點時,對城
的中點時,對城![]() 和城
和城![]() 的總影響度為0.065.
的總影響度為0.065.
(1)將![]() 表示成
表示成![]() 的函數.
的函數.
(2)討論(1)中函數的單調性,并判斷在![]() 上是否存在一點,使建在此處的垃圾處理廠對城
上是否存在一點,使建在此處的垃圾處理廠對城![]() 和城
和城![]() 的總影響度最小?若存在,求出該點到城
的總影響度最小?若存在,求出該點到城![]() 的距離;若不存在,請說明理由.
的距離;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】國內某汽車品牌一個月內被消費者投訴的次數用![]() 表示,據統計,隨機變量
表示,據統計,隨機變量![]() 的概率分布如下:
的概率分布如下:
|
|
|
|
|
|
|
|
|
|
(1)求![]() 的值;
的值;
(2)假設一月與二月被消費者投訴的次數互不影響,求該汽車品牌在這兩個月內被消費者投訴![]() 次的概率.
次的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
在平面直角坐標系![]() 中,直線
中,直線![]() 的參數方程為
的參數方程為![]() 為參數).它與曲線
為參數).它與曲線![]() 交于
交于![]() 兩點.
兩點.
(1)求![]() 的長;
的長;
(2)在以![]() 為極點,
為極點, ![]() 軸的正半軸為極軸建立極坐標系,設點
軸的正半軸為極軸建立極坐標系,設點![]() 的極坐標為
的極坐標為![]() ,求點
,求點![]() 到線段
到線段![]() 中點
中點![]() 的距離.
的距離.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com