Question

【題目】已知函數f（x）=（x﹣ ）ex ， g（x）=4x2﹣4x+mln（2x）（m∈R），g（x）存在兩個極值點x1 ， x2（x1＜x2）．
（1）求f（x1﹣x2）的最小值；
（2）若不等式g（x1）≥ax2恒成立，求實數a的取值范圍．

Answer 1

【答案】
（1）解： ，

令g'（x）=0得8x2﹣4x+m=0①，

因為g（x）存在兩個極值點x1，x2（x1＜x2），

所以方程①在（0，+∞）上有兩個不等實根x1，x2，

所以 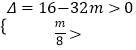解得 ，

且 ，

所以 ，

當 時，f'（x）＜0，當 時，f'（x）＞0，

所以f（x1﹣x2）的最小值為

（2）解：）由（Ⅰ）可知， ，

由g（x1）≥ax2得 ，

所以

=

=

=

=

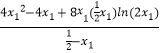
令（x）= （ ），

則'（x）=

因為 ，

所以 ，φ'（x）＜0，即φ（x）在 遞減，

綜上，實數a的取值范圍為（﹣∞，﹣3﹣2ln2]

【解析】（1）求出函數的導數，求出極值點，g（x）存在兩個極值點x1 ， x2（x1＜x2），推出 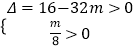，求出m的范圍，化簡x1﹣x2 ， 通過 時，f'（x）＜0，當 時，f'（x）＞0，求解f（x1﹣x2）的最小值．（2）通過g（x1）≥ax2得 ，化簡 = ，構造（x）= （ ），求出導函數，利用函數的單調性求解最值即可．
【考點精析】本題主要考查了函數的極值與導數的相關知識點，需要掌握求函數的極值的方法是:（1）如果在附近的左側,右側,那么是極大值（2）如果在附近的左側,右側,那么是極小值才能正確解答此題．